統計分析 ナースの統計学...医学検査の統計学...臨床医家の統計学........非線形モデル...................薬剤師の統計学
.....パネル分析
「下図はクラスター分析とデンドログラム」
統計分析の方法に迷ったら私達にメールしてみて下さい。ユニークなアイデアをご提供できるかも知れませんよ。
ご依頼とお問合せは、終了しました。
Statistical Analysis
note:分析依頼の資料を見ますと分割表などにデータが整理されています。しかし、原データを見ますと別の方法で検討すべき
ではないかと思ったりします。又、偏りの著しいデータなどでは、もっとデータを集めてから検討して欲しいと思ったりします。
でも、熱心な研究を思うと忌憚のないアドバイスに傷つきはしないか・・・、迷います。
教師の統計学......ビジネスの統計学.....社会現象の統計学(1)...社会現象の統計学(2).....薬効分析の統計
教師のための統計学って?
学校教育や社会教育の現場で必要なものは?
そうですね! 特に学校教育の現場では先生方の経験的な知識が大切にされているようだけど、その経験的知識にもとづく自信とアクションは客観的なデータの把握にあると思います。
生徒の学力考査にしても生徒のデータを情報として把握するには統計的な処理が求められる訳ですよネ。
データは単なる数値の羅列だけど統計分析によって、それは一人一人の生徒の情報へと変わります。
情報は先生の自信となり教育研究や教育現場での適確な方向性と問題解決の指針を与えてくれます。
最近では、 表計算ソフト(エクセルやロータスなど)の普及で簡単に統計分析が出来るようになりました。
でも、 多くの先生が統計手法の選択に迷っているようだけど・・・、大丈夫、
私達にメールして下さい。最適な手法をご一緒に考えましょう。
もちろん、 データを送信していただければ統計分析を行います。
分析を依頼するときは分析費用(見積もり)を確認して下さい。
大丈夫! 費用はやさしいし、クライアントと共に考え問題解決に努力します。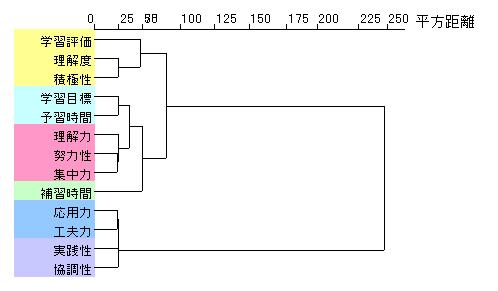
経営や営業でもっと統計手法を多用しましょう。
中小商工業者のための統計手法や営業企画販促での統計分析は、
1.販売実績の多角的な予測
2.事業、需要、競争の予測
3.販売商品の分類と予測
などですが、
マーケティングの統計分析はマーケティング・サイエンスとして、またオペレーション・リサーチとして経営戦略の重要な位置を占めている様に思います。
マーケティング・サイエンスは経営戦略の問題を解く科学としてマーケッターには欠かせないものだと思います。
下図はマーケティングで良く用いられる統計手法です。

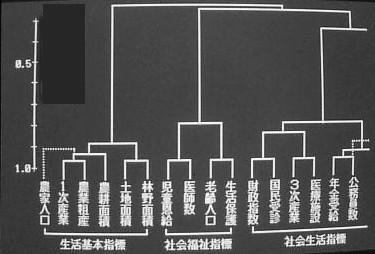
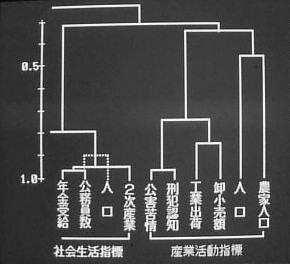
民力指標のクラスター分析(一例)
民力指標のデータをもとにクラスター分析(ウォード法)を行うと興味深いデンドログラム(樹枝図)が見られました。
例えば、「生活基本指標」と「産業活動指標」からこの県は多分に農業県だろうと想像することが出来ます。又、公害苦情件数と
刑犯認知件数が非常に近いところにあり、一時期には臨界工業地帯の公害問題がクローズアップされていたことがありますし、
その時期には工業活動が盛んで刑事事件も多かったようです。
「社会福祉指標」を見てナルホドと納得してしまいます。ところで「社会生活指標」で年金受給者数と公務員数が非常に近いところに
ありますが、どうしてでしょうか?
スギ花粉飛散の地域的な特徴について。
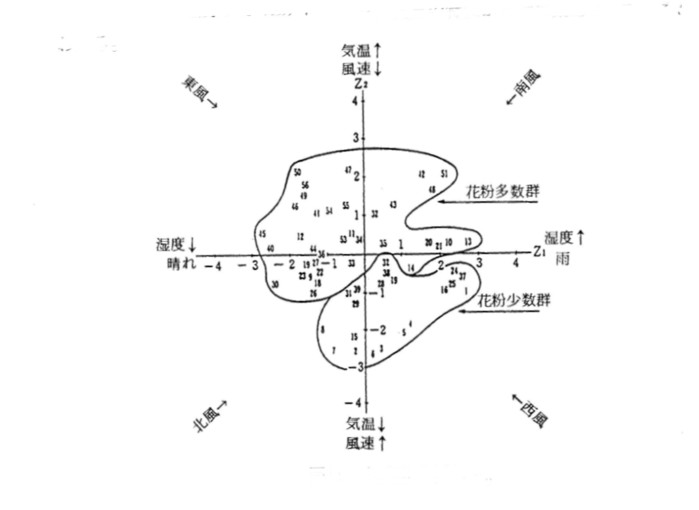
スギ花粉の飛散にかかわる多くの諸条件を包括した総合的な地域の特徴を抽出するためにある観測期間のスギ花粉飛散数と
気象データをもとに主成分分析を行ってみました。
主成分分析の結果は下図の散布図のようにスギ花粉飛散は少数群と多数群の2群に明瞭に分別されています。
第1主成分軸(横軸)と第2主成分軸(縦軸)に集約された指標として「気温と風速」、「湿度と天気・風向」の因子を見ることが出来ます。
相対的に、多数飛散の条件は「気温が高く穏やかな東風または南風の晴れまたは曇りの日」に、少数飛散の条件は「気温が低く西風または北風の雨の強い日」で
あることが分ります。
至極当然と言えば当然ですが、当然の事を証明してみるのも統計分析ではないでしょうか。
生物学的同等性の検証って・・・?
統計的な有意差検定のほとんどは、「有意差がある」ことを帰無仮説として検定を行いますよネ。ところが、「有意差がない」ことを積極的に期待して有意差検定を行うこってあるの・・・?
薬効データの分析などではよくありますよ!
生物学的同等性試験「Bioequivalency(BE)」がそうです。そうです・・・、治験薬と対象薬の効果の検証ではその効果に差のないこと「同等である」(同等性)あるいは「劣らない」(非劣勢)ことが問われます。
この様な検証を negative trial と呼んでいます。通常の有意差検定は帰無仮説を間違って否定する確率(有意水準)を保障しているのであって、対立仮説である「差がない」ことを保障しているのではありません。
だから、「差がない」は「差がないかも知れない」なのです。