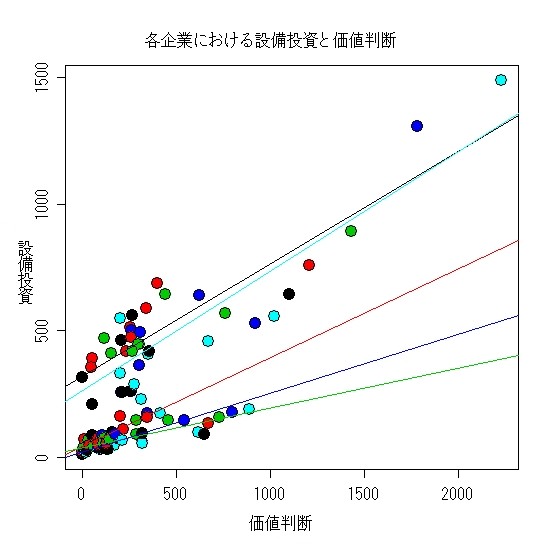
統計分析 ナースの統計学...医学検査の統計学...臨床医家の統計学........非線形モデル...................薬剤師の統計学
.....パネル分析
Statistical Analysis
note:依頼者によっては、SPSSでの結果を希望されますので柔軟に対応しています。SPSSは世界的に有名なソフトだけど日常的には使い慣れたソフトで対応しています。
教師の統計学......ビジネスの統計学.....社会現象の統計学(1)...社会現象の統計学(2)
...薬効分析の統計
ナースの統計学
ナースのための統計学って?
医学関係の統計手法とどうちがうの?
そうね! 統計の方法に違いはないのだけど、ヤッパリ、ナース学会での研究発表やナース関連の学術誌で発表されている研究内容を拝見すると看護現場での調査研究などが多くて、医学実験的な研究は少ないようです。
だとすると、 当然、統計の手法選択に違いがあってもおかしくないでしょう。
最近では、 表計算ソフト(エクセルやロータスなど)の普及で簡単に統計分析が出来るようになりました。でも、 多くのナースが統計手法の選択に迷っているようだけど・・・、大丈夫、
私達にメールして下さい。最適な手法をご一緒に考えましょう。
もちろん、 データを送信していただければ統計分析を行います。
まずは、分析費用(見積もり)を確認して下さい。
大丈夫! 費用はやさしいし、ご予算内での検討もご相談下さい。
医学検査の統計学って?
特徴的な統計手法は、やっぱり、精度管理? 品質管理(QC)の精度管理の手法が元になっていますが、いつまでも品質管理の手法では現代医学の検査にマッチしないのではないでしょうか? 平均値や標準偏差での表現は、わかり易いけど、これは正規分布が元になっていることはご存知の通りです。正規分布にならないデータの方が多いのに、おかしくはないですか。 情報理論を適用して医学における精度管理を考えませんか。 私達は「ネットワーク・ラボラトリー」です。医学検査や医学研究でのデータ分析に気軽に利用できます。
しかし、いきなりデータをメールで送りつけるのはマナー違反・・・・。 統計分析の方法とか、目的とする分析結果などをメールでご相談下さい。統計分析を依頼するときは「見積もり」を取って下さい。
費用はやさしいし、見積もり内で検討しご納得いただけます。
最近では、密に利用しているみたいで宣伝していただけないのが残念です。
でも、喜びのメールを見ると採算など度外視してしまうのが商売下手なのでしょう。
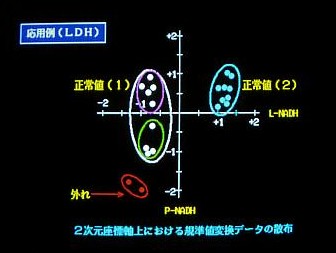
臨床医家の統計学って?
医学研究の成果を論文や学会で発表するとき、必ずと言っていいほど、統計分析の方法が適切であるか、どうかがレフリーの厳しい目にさらされます。 高価な統計分析ソフトを使ったからって、いい結果が得られるものではありません。 最近のレフリーは、統計分析の不備を容赦なく指摘してきます。 医学での統計的仮説は、QCでの仮説とはチョッと違うのだと思います。医学では探索的な統計手法が多くて、 検定方法の解釈もチョッと違うようです。パラメトリック検定からノンパラメトリック検定を積極的に多用するようになったのも、医学データでの分布の多くが正規分布でないことによると思いますが、 分布に依存しない統計手法としてのノンパラメトリック検定や多変量解析などがモット多用されても良いように思います。
どうでしょうか? 統計分析の手法とか方法に迷ったら私達にメールしてみて下さい。当研究所のご利用者の多くは医学者なのですから。
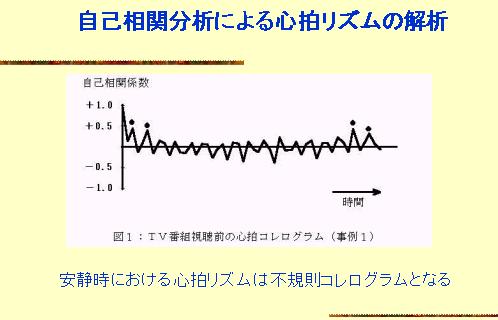
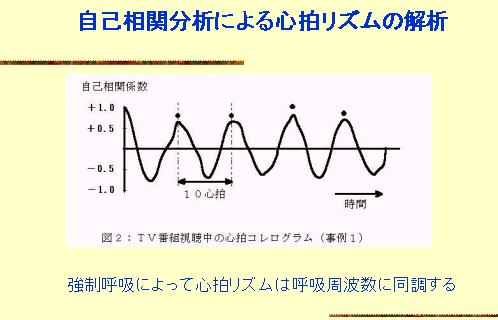
100心拍のRR間隔時間を用いて自己相関分析(AutoCorrelation)を行いますと、上図のような不規則な波形(コレログラム)となります。
次に同一被験者について1分間 10回のゆっくりした数息間呼吸、例えば座禅時の呼吸を行わせると不規則であったコレログラムが下図のような規則的なコレログラムになります。
これは呼吸周波数に心拍リズムが同調したことを表しています。すなわち深くゆっくりとした数息間呼吸によって心身がリラクッスした状態となります。
この様なリラクリレーションは副交感神経機能試験として知られているところですが自動解析の心電図ヒストグラム解析よりも分かり易いと思いますが。
医学での非線型モデルと言えば、すぐに多重ロジスティック、指数ワイブル、そしてCox比例ハザードモデルなどが頭に浮びますよネ。
ところが、最近ではパソコンで簡単に分析できる統計ソフトの普及で、データをよく吟味することなく分析していませんか。
ここでは、簡単な仮想例題のCoxハザードモデルを示しておきましょう。
例題は、骨髄性白血病患者(30例)の「生存期間」、「白血球数」、「白血球タイプ(M1,M2)」、「転帰(生、死)」を変数とします。
Cox比例ハザードモデルによる生存関数は次の通りです。
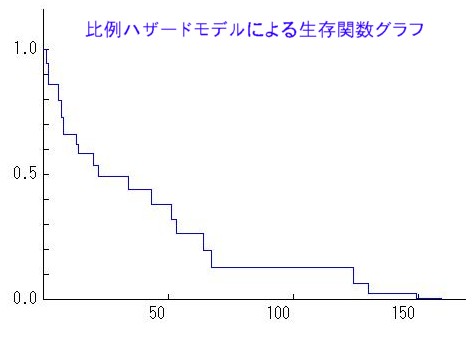
そして、分析結果として得られる主な統計値は次の通りです。
| 変数 | 推定値(β) | 標準誤差 | χ2乗値 | p値 | exp(β) |
| 白血球数 | 0.0000141 | 0.0000065 | 4.651 | 0.031 | 1.000 |
| 白血球タイプ | 1.329 | 0.4955 | 7.194 | 0.007 | 3.777 |
ここで、「標準誤差」が「+」の時はハザードが大きくなること、すなわち、死亡の増加に寄与していることを表します。 逆に、「−」の時は死亡に対して抑制的であることを表しています。 また、exp(β)はOdd比を表しており、一般に相対ハザードと呼ばれているものです。
そして、Cox比例ハザードの検定は「β≠0」について行うもので、代表的なものに尤度比検定(-2LOG L)があります。 ここでの例題の尤度比検定(-2LOG L 、自由度=2)は10.62(p=0.005)であり、「β≠0」と言えます。
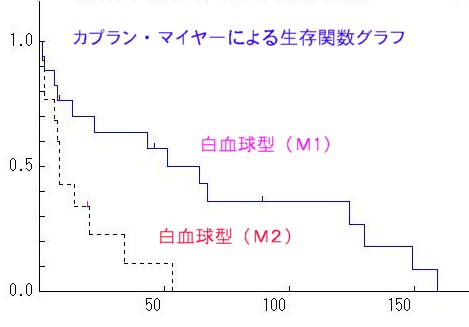
2群の生存率関数グラフではカプラン・マイヤ(Kaplan-Meier、KM)法がよく用いられますが、KM法は標本数がせいぜい50例以下に適用します。 しかし、パソコンではどんなに大きなデータでも簡単に結果が出せますので、安易に使用してはいませんか。
大きな標本での生存率の検定は「Cutler-Ederer」、「Chaiang」、「Littel」なども検討しましょう。 ここでの仮想例題では白血球タイプを「M1」と「M2」の2群に分けてKM検定を行ってみました。
KM法でのグラフを見ますと、明らかに「M1>M2」となっています。この2群での生存率の検定では次の結果が得られました。
・「Generalized Wilcoxon検定」:χ2乗値=4.653(p=0.031、有意)。
・「Log-Rank検定」:χ2乗値=7.646(p=0.006、有意)。
KM法においても、また、他の方法においても打ち切り(生存)例があまりに多いときは、データのバイアスがもたらす影響を考慮すべきです。
何でも簡単にパソコンに依存すると、その結果に基く次のアクションを不確かなものとしますよ。依頼者には遠慮がちになるけど、本当の親切って・・・、難しいよネ。
薬剤師の統計学って?
薬効とか、薬物体内動態とか、薬物体内速度とか、薬学分野の統計手法もナノテクノロジーの発展で従来の薬物論では間に合わなくなってきていると思います。 単純な1次式あるいは2次式などのコンパーネント・モデルを当てはめるのは無理なようです。 ほとんどが非線形問題や情報理論の適用が求められるようになったと思いますがどうでしょうか。 そうは言っても、薬効解析における分割表形式のカテゴリカル検定は重要ですね。 しかし、分割表にまとめる過程に多くの主観が入り込んでいると思いませんか?
例えば、
有効・無効の分割表においても、これを客観的に分類するなら、どうしても多次元データでの解釈が必要になります。 要するに、多変量解析によって客観的に分別されなければならないって訳です。 分割表検定の手法は色々と解説されているけど、分割表にまとめる手法についての解説は少ないように思いますが?
統計分析の手法とか方法に迷ったら私達にメールしてみて下さい。

映画「ロレンッツオのオイル」より。