すぐに役立つ統計のコツ〜医学統計編〜

当研究所には、色々な統計的問題の相談や依頼が寄せられます。最近の特徴は、海外の学術誌への投稿が多くなり、
査読者（Reviewer）の native な専門用語による統計的方法の指摘に悩む場合もあるようです．
最も多いのが、正規分布（等分散性）を仮定したパラメトリック検定に対する指摘であり、正規性検定が求められる事です．
また、相関回帰分析などにおける多重共線性の指摘や、一般化線形モデルの分析を求められる様になって来ました.
多重共線性の影響を調整したリッジ回帰分析や主成分回帰分析など、今まで馴染のなかった方法に戸惑う事も多くなっています．
特に、反復測定データでの線形混合効果モデルや共分散分析などは、最近の医学統計に欠かせない手法になっています．
その他にも、機械学習やベイジアンなど、次々と２１世紀の分析手法が登場して来ており、医学分野への応用も急速な広がりを見せています．

そこで本書では、
　・査読者からよく指摘される正規性検定の方法と、その結果に基づく検定方法の選択を示しています．そして、
　・非正規と判断されたら、積極的にノンパラメトリック検定を用いることを勧めています．
　・しかし、むやみやたらにノンパラメトリック法の使用を勧めている訳ではありません．
　・対数変換によるパラメトリック検定の事例もデータの吟味によって適用の可否を決めるべきです．
　・相関と回帰分析でも対数変換の事例を示していますが、データの本来の姿(曲線分布)が大切なこともあります．
　・多重共線性を考慮した相関回帰分析や臨床検査における精度管理(検量線)などを例示しています．
　・また、分割表形式にまとめられたデータの度数（比率）の検定も詳しく紹介しています。
　・MS-Excel では困難な統計的問題は、インターネット環境を利用したフリーオンラインソフトの利用を紹介しています。
　・本書で紹介したフリーオンラインソフトは、データ解析環境「Ｒ］に基づいており信頼出来るでしょう．

本書の特徴は、
　・MS-Excel を基本とした例題による分析．
　・フリーオンライインソフトを利用した例題による分析．

などを中心に、実例をもとに紹介しています．

統計の専門職はともかく、統計学を履修中の学生であっても、高価な商用統計ソフトを個人で購入するには荷が重いかも知れません．
体験版とか、試用版とかの商用ソフトを使えば良いのですが、必要肝心な折りに期限切れだったりして・・・、腹立たしい思いをした経験者もいるようです。
ハッキリ言って、専門職でない限り、商用統計ソフトの使用頻度は低いと思われます．しかし、
必要なときに統計学的な知識が無かったら、大切な研究論文をまとめる事さえ出来ないでしょう．そこで、
本書が手元にあれば、その大切な時に開いて下さい．その為にも一度はざーっと目を通しておいて欲しいものです！

訂正と加筆：

正誤表：

ページ	誤	正
14ページ	正規性検定(Shapiro-Wiilk test)	Shapiro-Wilk test
47ページ(下から4行目)	OR={a/(a+c)}/{b/(b+d)}	{(a/c)/{b/d)}
50ページ(下から4行目)	第3章	第4章
52ページ(図5.1)	60才未満と60才〜70才未満[*]	60才〜70才未満と70才以上に[*]
74ページ(上から14行目)	回帰係数(切片と勾配)	回帰係数(勾配)
76ページ(表6.6)	表36	表6.5
85ページ(常用対数変換濃度)	プリントミス	本ページ下方参照
89ページ(下から6行目)	表6.14	表6.15
90ページ(下から3行目)	systemic erroe	systemic error
90ページ(下から2行目)	randam erroe	random error
91ページ(図6.15)	randam error	random error
91ページ(下から5行目)	Systemic erroer	Systemic error
91ページ(下から3行目)	Randam erroer	Random error
101ページ(下から8行目)	二元配置法が	二元配置法を
111ページ(上から５行目)	←	十字

表3.5(15ページ)　検定統計量の出力結果（行列補完）

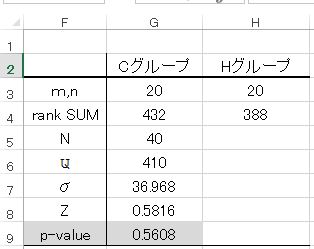
図3.3(17ページ)　表3.2のGPTにおけるBoxPlotと検定結果（一部修正）

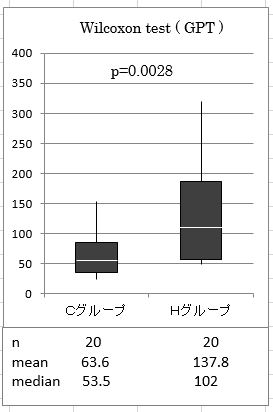
表5.2　データレコードの理化学(量的)データ(41ページ)の年齢(Age)の訂正

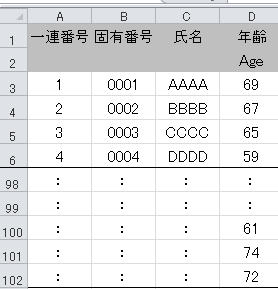
表5.16　年代別のコレステロール(200以上)の比較
行列の関数式：
--------------------
D3：=E3−C3
D4：=E4−C4
D5：=E5−C5
--------------------

表5.22（56ページ）　アスベストと胸部レントゲン像（訂正）

-----

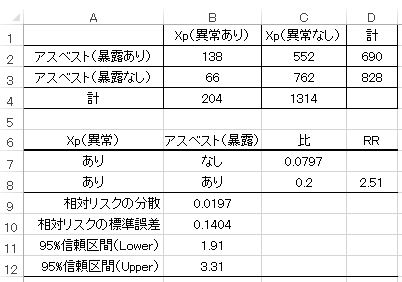
本書の６章(84ページの下から２行目の「X0=SQRT(4a(c-Y0))/2a」は Excel関数を使って次により計算します．
(SQRT(ABS(b^2-4a(c-Ｙ0))-b)/2a

例えば、
図6.10では Ｙ=-5E-07�]^2＋0.0015�]＋0.084 ですので、
a=-0.0000005、b=0.0015、c=0.084 を当てはめて計算します。

そして、
吸光度(Ｙ0)＝0.5 に相当する濃度(x)は、上記の式に当てはめるとx＝309.2 となります。

なお、
常用対数変換濃度(log�])は、次の様に訂正をお願いします。
1.362 1.663 1.964 2.255 2.568 2.869 3.176 ← 正

上記と同様に、
a=0.2566、ｂ=-0.554、c=0.336 を当てはめると、

吸光度(Ｙ0)＝0.5 に相当する対数濃度｢Log(x)]は、Log(x)＝2.423 となります。
もとの濃度は、10^2.423≒265 となります。

当てはめがよければ、なるべく実測データから逆推定しましょう。

補完事項：

第７章 多次元データを比較する(多変量解析)
表7.17（105ページ）
分散分析表（例題17）の”誤差”は表７.12（手順１）の”残差（45227）”です。

３. ２値データを複数のデータで説明する〜ロジスティック回帰分析〜

110ページ
Event＝-1.57＋2.029×X1＋1.919×X4

上記の計算式は、

log(p／(1-p)＝Event＝-1.57＋2.029×X1＋1.919×X4

のロジスティック回帰モデルとなり、ｐは次のExcel関数で求めます。

p＝exp(Event)／(1＋exp(Event))

ロジスティック回帰モデルによる予測(判別)は 116ページ を見て下さい。

ユークリッド距離の計算（121ページ）
ユークリッド距離の計算においても各変数の単位が異なるときは、118ページ(上から4行目)の様に
データの標準化「(各変数測定値−各変数の平均値)/各変数の標準偏差」により、単位を同じにして
計算した方がよい時もあります。

● 主成分分析：フリーオンラインソフトを利用する（128ページ）の要領を説明します。
アクセス先(URL)：https://www.wessa.net/stat.wasp

以下によりデータを入力し実行します。
Factor Analysis(click)→Rotated Factor Analysisi(click)→
本書(128ページ)の要領でデータを入力→Compute(click)