戻る　　　　　次へ　　　　　目次へ

９．雑記
gooブロッグに投稿してきた「医学と統計(1)〜(81)」を編集し、統計分析の具体的な事例をもとに、その手法を説明する。
近年、優れた商用統計分析ソフトの普及により、電卓などによる筆算すら必要なくなってきている。しかし、その手法を誤ったとしても分析ソフトはそれらしい結果を出力するので注意が必要である。
この章は、前章までの手法の補足的あるいは忘備的に記録しておくものであり、統計学的な理論性は一切記述していないので、必要に応じ本書の各章などを参考にされたい。
ここでは、主としてデータ解析環境「R」を用いている。

9.1. 順序カテゴリーによる分割表の出現率の検定について。
医学と統計(6)投稿から。

L行×M列の分割表におけるカイ二乗検定で有意差が出れば有意差のある組み合わせを検討します。
すなわち、
２×M列であれば、どの行に有意差が有るかを調べる必要があります。ここでのカイ二乗検定は出現比率（度数）の差の検定ですが、もし、 その比率（度数）に何らかのトレンド（傾向）があると順序カテゴリーの分割表として扱われます。
順序カテゴリーとは「満足」「やや満足」「普通」「やや不満」「不満」などとか、「-」「+-」「+」「++」「+++」 とか言った大きさや順序がある分割表にまとめられたものです。

例えば（引用：すぐわかるEXCELによるアンケートの調査・集計・解析[第２版]、内田治、東京図書、2002.6.25、p164）、

性別	不満	やや不満	どちらでもない	やや満足	満足
男性	5	15	35	30	15
女性	10	25	30	25	10

このデータを通常のカイ二乗検定を行うと、
カイ２乗値＝6.0058、自由度＝4、p値＝0.1987

となり有意差がないと判断されます。

「R」での実行
mydata <- matrix(c(5, 15, 35, 30, 15, 10, 25, 30, 25, 10), nc=2, byrow=F)
mydata
chisq.test(mydata)　

しかし、
このデータの出現率には単調な傾向（不満＜満足）がありそうです。
そこで、
傾向性仮説（コクラン=アーミテージ：Cochran-Armitage）の検定を行ってみると、

カイ２乗値（trend）＝4.9221、自由度＝1、p値＝0.02651

で有意差が認められ、男性と女性の傾向には差があると判断されました。

「R」での実行
male <- c(5, 15, 35, 30, 15)
total <- c(15, 40, 65, 55, 25)
prop.trend.test(male, total)

男性（male%）と女性（female%）の傾向性をグラフにして見てみましょう（図１）。

図１：男性と女性の傾向性

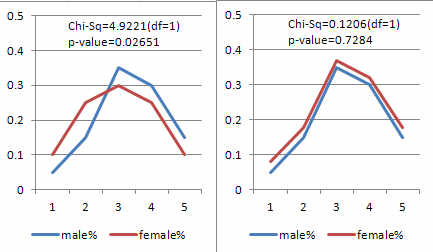
左図が元々のデータの比率ですが、この比率を右図の様に変えて見ますと、
Cochran-Armitage の検定結果は次の様になりました。

カイ２乗値（trend）＝0.1206、自由度＝1、p値＝0.7284 　

すなわち、
男性と女性の傾向には差がないと判断されます。

この様に、順序を伴った変化を調べるときは、ここでの傾向性の検定の適用を考えて見ましょう。

例題として、4章（百分率を比較する）の 「4.3.2（ｂ．傾向を有するとき）」の「例題１２」をデータ解析環境「R」でおこなってみましょう。

「R」での実行
ABN<- c(2, 3, 4, 5, 8) #ST・T 異常出現数
OBS<- c(100, 100, 100, 50, 50)　#対象数

prop.test(ABN, OBS)
X-squared = 16.5464, df = 4, p-value = 0.0024

この結果から、
負荷心電図検査において、運動時間によってST・T 異常の出現比率に有意差があると判断されます。
しかし、
その比率が直線的に増加するかどうかは、次の検定結果をみなければ分かりません。

prop.trend.test(ABN, OBS)
X-squared = 13.7297, df = 1, p-value = 0.0002

この結果は有意であり、傾向性を表す勾配がゼロ「0」でない、すなわち、傾向を有すると判断されます。

4章（百分率を比較する）の「例題12」では、ST・T の異常出現が１次関数的に増加するかどうかの検定があります。
「R」では、
次のURLへアクセスして「Rプログラム」を利用させて頂きましょう。
（群馬大学　青木繁伸教授）

出力結果は次の通りです。

統計量	カイ二乗値	自由度	P 値
トレンド	13.729	1	0.0002
直線からの乖離	2.8166	3	0.4207
非一様性	16.546	4	0.0023

この「Rプログラム」を実行すれば、個々に、「prop.test」や「prop.trend.test」を用いなくても、 必要な統計量が一気に出力されます。
出力結果の「トレンド＝prop.trend.test」、「非一様性＝prop.test」の結果と同じです。
「直線からの乖離」は、
ST・T 異常出現率の予測値と実測値との乖離を表しており、有意でないので、その差は小さいと言えます。
すなわち、１次関数的に高くなると言えます。

ノンパラメトリック法の「Wilcoxon の順位和検定」を用いる場合は、下記の Webオンラインソフトが便利でしょう。

使用方法に従って入力すると、次の結果が得られました。

カテゴリー	第一群	第二群	合計	平均順位
第1カテゴリー	5	10	15	8.0
第2カテゴリー	15	25	40	35.5
第3カテゴリー	35	30	65	88.0
第4カテゴリー	30	25	55	148.0
第5カテゴリー	15	10	25	188.0
合計	100	100	200	...

順位和＝10912.5
期待値＝10050.0
分散＝156532.66
Z=2.1787

検定結果： 0.01 < P < 0.05
危険率：0.0293

戻る     次へ      目次へ     TOPへ