9.2. 薬剤効果の同等性の検証について(有効率の場合)。
医学と統計(7)
(80)
(81)投稿から。
いくつかの例題で実際の手法を説明しましょう。
例題1
| 効果 | 著名改善 | 改善 | やや改善 | 不変 | 悪化 |
| A薬剤 | 5 | 23 | 19 | 15 | 4 |
| B薬剤 | 4 | 14 | 26 | 21 | 1 |
この例題1 は、「医薬統計解析マニュアル、斧田太公望、メディカルリサーチセンター、1988」から引用させていただきました。
ノンパラメトリック法による有意差検定は「前項(9.1.)」の Webオンラインソフトを利用させていただきましょう。
例題1の出力結果は次の通りです。
順位和= 4142.5
期待値= 4389.0
分散= 44308.1679
Z= 1.16867
検定結果: P > 0.05
危険率: 0.2425
よって、
A薬剤とB薬剤の効果には有意差が認められません。
ちなみに、
ここでは有意差を期待して検定を行ったのでしょうか?
あるいは、
差のないことを期待して検定したのでしょうか?
例えば、
後発薬のように先発薬との有効性に差がないことを期待しての検定ならば、効果に差のないことを積極的に証明しなければなりません。
ここでの検定で有意差がなかったからA薬剤とB薬剤の効果は同等であるとは言えません。
通常の検定は帰無仮説が棄却できるかどうかを問うもので、これを positive trial と言っています。
例えば、
「容疑者=真犯人」として裁判中にアリバイが成立すれば無罪となるように、確率的に一定の有意水準を設定して有意差を決めている
訳です。
検定で有意差がなかったから「同等である」とは言えません。
では、
積極的に「同等である」と言うにはどうすれば良いのでしょうか。
この様な問題を negative trial と呼んでおり、検定ではあらかじめハンディキャップをつけて検定をスタートさせます。
同等であれば、
スタート時点でハンディを付けているのですから、ハンディの差のままゴールする筈です。
ここでは、
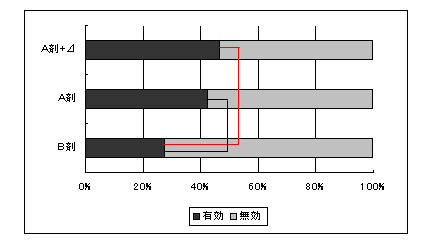
A剤の有効率は「著名改善+改善=28(0.4242)」であり、これを「被験薬」とします。
B剤の有効率は「著名改善+改善=18(0.2727)」であり、これを「対照薬」とします。
では、次の要領(ハンディキャップ法)で検証してみましょう。
まずは、
比率差の検定をWebオンライソフトを利用して行っておきましょう。
データの入力
Two proportion Z-test caluculator
calculator
| ... | Sample 1 | Sample 2 |
| Proportion | 0.4242 | 0.2727 |
| Sample size | 66 | 66 |
Alpha...0.05
Variance...◎Equal
Tail...◎Both
出力結果
result
Z-value = 1.8265
Two-tailed p-value = 0.0678
以上の結果から有効率(対照薬と治験薬)に差がないと判断されましたので、次により非劣性(同等性)の検証を試みます。
Xa=A剤の有効数、Xb=B剤の有効数、Na=A剤の例数、Nb=B剤の例数、マージン=0.1(10%)
として、下記に簡易計算法を示します(正確な計算方法は専門書を見て下さい)。
P=( Xa+Xb+Na*0.1 )/( Na+Nb ) = ( 28+18+66*0.1 )/( 66+66 ) = 0.3985
F.left=(P-0.1)*(1-P+0.1)/Na = (0.3985-0.1)*(1-0.3985+0.1)/66 = 0.00317
F.right=P*(1-P)/Nb = 0.3985*(1-0.3985)/66 = 0.00363
SE=sqrt(F.left + F.right) = sqrt(0.00317 + 0.00363) = 0.0825
U=(Pa - Pb+0.1) /SE = (0.4242 - 0.2727+0.1)/0.0825 = 0.2515/0.0825 = 3.049
U = 3.049 > Z(0.05) = 1.645 (危険率5%)
であるので、マージン(10%)の差をつけて検定し有意差が認められました。すなわち、
10%以上劣ることはない、同等性が認められたと言えます。
95% 信頼限界は、
(Pa-Pb) ± 1.96*SE = 0.1515 ± 1.96*0.0825 = -0.0102 〜 0.3132
−Δ = -0.1 < Lower 95%CI = -0.0102
ですので、検定結果と同じく「非劣性」であると言えます。
例題1のA薬剤とB薬剤の対照薬と被験薬を逆にして計算してみましょう。
P = 0.3985
F.left = 0.00317
F.right = 0.00363
SE = 0.0825
U=(Pa - Pb+0.1) /SE = (0.2727 - 0.4242+0.1)/0.0825 = -0.6242
U = -0.6242 < Z(0.05) = 1.645 (危険率5%)
マージン(10%)では、有意差が認められませんので同等とは言えません。
マージン(29%)では、
U=1.6788>Z(0.05) = 1.645 (危険率5%)
ですので、
29%以上劣ることはないとなります。ハンディキャップとして29%が妥当であるかどうかは議論のあるところです。
通常は10%のハンディキャップを用いることが多いようです。
戻る 次へ 目次へ TOPへ