- 仮説でのμA,μBは,2つの母集団での分布関数FA(x),FB(x)の平均値とする.
- 仮説について云えば,2つの母集団からの分布関数をFA(x),FB(x)とするとき,
帰無仮説(H0):FA(x)=FB(x):FA(x)/FB(x)=1 に対して検定を行うことになる.
「ノンパラメトリック検定」では,以下同じ様な意味である. - 昇順順位系列とは,データを小さい方から大きさの順に並べたものを云う.
- 検定統計量(R0,U0)は順位和の小さい方である.
- データに同じ順位のものがあるとき,順位の平均をそれぞれのデータに与える.
実際の要領は「例題21」を参考にされたい. - A群とB群のデータの個数の小さい方をnA,大きい方をnBとする.すなわちデータの個数はnA≦nBの関係とする.
ここでの「エクセル関数式」では大きさを考える必要はない. - T分布とU分布のパーセント点は,日本規格協会刊の「簡約統計数値表(ノンパラメトリック検定)」を参考にされると良い.
B. 対応のないとき(ノンパラメトリック検定)
平均値の差の検定において,2群でのいずれかの分布が,データ変換によっても正規性が得られないとき,
あるいは離散量データであったり,順位尺度で測られているようなときには,ここでの検定を用います.
ここでは次の2方法について説明します.
①ウイルコックスン(Wilcoxon )の順位検定.
②マンウィットニー(Mann-Whitney)の順位検定.
[一般形式]
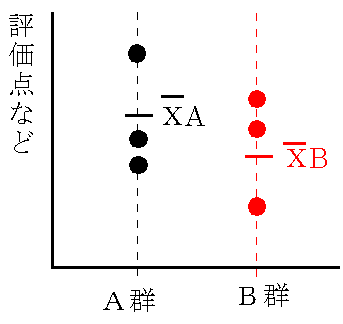
血圧を例にとれば,A群とB群は異なる薬剤などによって得られる評価の点数などです.
[検定の手順]
①検定の問題を明らかにする.
「2つの標本の平均値に差があるか?」
②仮説の設定を行う. 注釈表示
帰無仮説(H0):μA=μB
対立仮説(H1):μA≠μB.................(両側検定のとき)
対立仮説(H1):μA>μB, または μA<μB(片側検定のとき)
③危険率(100α%)を設定する.
両側検定の有意水準:α/2
片側検定の有意水準:α
④検定統計量(R0,U0)を計算する.
まず,初めにデータの符号化と順位変換を行います.
すなわち,A群とB群のデータをひとまとめにし,表23のような昇順順位系列を作ります.
注釈表示
このときnA=A群のデータ個数,nB=B群のデータ個数,XA=A群のデータ,XB=B群のデー タ (i=1,2,・・・,nA:j=1,2,・・・,nB : nA<=nB)とします.
| 順位 | r1<r2<・・rk・・・<rn | 順位和 |
| A群 | R1<R2<・・Rk・・・<Rn | RA |
| B群 | R1<R2<・・Rk・・・<Rn | RB |
R1~RnはA群とB群のそれぞれのデータ(XA,XB)の順位とします.
ここで,
RA とRB の小さい方をウイコックソンの検定統計量(T0)とします.
注釈表示
また、
マンウィットニーの検定統計量(U0)は,次のようになります.
UA=(nA・nB)+ nA(nA + 1)/2 - RA
UB=(nA・nB)+nB(nB + 1)/2 - RB
そして,
UAとUB の小さい方をマン・ウィットニーの検定統計量(U0)とします.
⑤統計的判定を行う.
[両側検定のとき]
T0>TnA,nB(α/2)または,U0>UnA,nB(α/2)ならば,
「危険率100α%で有意な差がない」
T0≦TnA,nB(α/2)または,U0≦UnA,nB(α/2)ならば,
「危険率100α%で有意な差がある」
[片側検定のとき]
T0≦TnA,nB(α/2)または,U0≦UnA,nB(α/2)ならば,
「危険率100α%で大きい(小さい)」
T(α/2),U(α/2)は 表計算ソフト(エクセル関数式)から求めます.
求め方は次の「例題21」を参考にして下さい。
[例題21]
気管支喘息患者にキサンチン誘導体製剤を投与し,その効果を「発作の改善性」,「患者の印象」について5段階評価した成績を表24に示します.
| 発作の改善性(標本A) | 5 , 3 , 2 , 4 , 4 |
| 患者の印象(標本B) | 4 , 2 , 1 , 3 , 3 |
評価点数に有意な差があるかどうかを検定してみましょう.
検定は次の手順で行います.
①標本(A)と標本(B)のデータ(点数)をひとまとめにして,大きさの順に並べ変えると表25のようになります.
| 順 位 | 1 , 2 , 3 , 4 , 5 , 6 , 7 , 8 , 9 , 10 |
| 標本(A) | ....2.......3...........4...4.......5 |
| 同一順位 | ....○......△..........□..□ |
| 標本(B) | 1.......2.......3....3..........4 |
| 同一順位 | .......○.......△...△........□ |
同じ順位のもの,
2点(○印)が2ツ
3点(△印)が3ツ
4点(□印)が3ツ
それぞれに順位の平均を与えます.
注釈表示
順位の平均は次のように計算します.
2点の順位平均=(2位+3位)/2=2.5
3点の順位平均= (4位+5位+6位)/3=5
4点の順位平均=(7位+8位+9位)/3=8
②検定統計量(T0,U0)の計算.
標本(A)と標本(B)の順位は表26のようになります.
| 標 本 | 順 位 | 順 位 の 和 |
|---|---|---|
| 標本(A)の順位 | 2.5 , 5 , 8 , 8 , 10 | RA=33.5 |
| 標本(B>の順位 | 1 , 2.5 , 5 , 5 , 8 | RB=21.5 |
ウイルコックスンの検定統計量(R0)は,順位和の小さい方(RB)の 21.5 が R0=21.5となります.
なお,マンウィットニーの検定統計量(U0)は,
標本(A>のデータの個数 nA=5,標本(B)のデータの個数 nB=5 ですので,
UA=(5×5)+(5×(5+1))/2-33.5=6.5
UB=(5×5)+(5×(5+1))/2-21.5=18.5
となります.
UA,UB のうち小さい方(UA)の 6.5 が検定統計量(U0=6.5)になります.
③「ウイルコックスンのT分布」と「マンウィットニーのU分布」から,それぞれの下側パーセント点を求めます. 注釈表示
パーセント点は表計算ソフト(エクセル関数式)から求めます。
ウイルコックスンの下側臨界値は次の「Wilcoxon%point」をクリックして下さい。(「Wilcoxon%point)
マンウイットニーの下側臨界値は次の「MannWhitney%point」をクリックして下さい。(「MannWhitney%point)
「エクセル関数式」では片側の%点が与えられますので、
危険率5%での両側検定では有意水準(α)0.05/2=0.025 のセルにA群とB群の個数を入力して下さい。
そうすると、
ウイルコックスンR(0.05/2)=17
マンウイットニーU(0.05/2)=2
が表示されます。これが危険率5%の両側%点(臨界値)となります。
ここでは、
R0=21.5>T(0.05/2)=17 (両側検定,危険率 5%)
U0=6.5>U(0.05/2)=2 (両側検定,危険率 5%)
から,標本(A)と標本(B)の評価点に有意な差はないと云えます.
すなわち,「発作の改善性」と「患者の印象」は一致していると考えられます.