- 暯嬒抣偺乽嵎乿傪専掕偺栤戣偲偡傞偲偒丆俀慻偺昗杮偺惓婯惈偼乽a.懳墳偺側偄偲偒乿傎偳丆尩枾偵峫偊側偔偰傕椙偄丏
偟偐偟丆惓婯惈偺壖掕偑嬌傔偰崲擄側偲偒偲偐丆惓婯暘晍偱偁傞偐偳偆偐暘偐傜側偄偲偒偵偵偼乽D丏僲儞僷儔儊僩儕僢僋専掕乿傪梡偄傞丏
俠丏懳墳偺偁傞偲偒乮僷儔儊僩儕僢僋専掕乯
乽懳墳偺偁傞偲偒乿偲偼丆俀慻偺僨乕僞偑塣摦偺慜屻偲偐丆搳栻偺慜屻側偳丆専掕偺懳徾偑堎側傞帪揰偱應傜傟偰偄傞傛偆側傕偺傪塢偄傑偡丏
傑偨丆俀慻偺僨乕僞偑堎側傞曣廤抍偐傜偺傕偺偱偁偭偰傕丆摨堦忦審壓偱儁傾偲偟偰應傜傟偰偍傝丆摨堦偺摿惈傪桳偡傞傕偺偼乽懳墳偺偁傞偲偒乿偲偟偰埖偊傑偡丏
乵堦斒宍幃乶
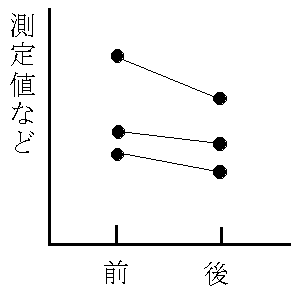
寣埑傪椺偵偲傟偽丆俙孮偲俛孮偼摨偠屄懱偵懳偡傞栻嵻偺搳梌慜屻丆偁傞偄偼塣摦偺慜屻側偳偱偡丏
乵専掕偺庤弴乶
嘆専掕偺栤戣傪柧偐偵偡傞丅
拲庍昞帵
乽俀偮偺昗杮偺暯嬒抣偵嵎偑偁傞偐丠乿
嘇壖愢偺愝掕傪峴偆丅
婣柍壖愝乮俫0乯丗兪A亖兪B
懳棫壖愝乮俫1乯丗兪A亗兪B 丂丂丂丂丂 乮椉懁専掕偺偲偒乯
丂
懳棫壖愝乮俫1乯丗兪A亜兪B 傑偨偼 兪A亙兪B乮曅懁専掕偺偲偒乯
嘊婋尟棪(100兛亾)傪愝掕偡傞丅丂
椉懁専掕偺桳堄悈弨丗兛丂
曅懁専掕偺桳堄悈弨丗2兛
嘋専掕摑寁検(倲0)傪寁嶼偡傞丏
弶傔偵,俀孮僨乕僞偺嵎(倓i)偲嵎偺暯嬒(倓bar乯傪寁嶼偟傑偡丏 倓i亖倃Ai亅倃Bi 倓bar亖嚁倓i乛値
偦偟偰丆師偵僨乕僞偺嵎偺暘嶶(倁)傪寁嶼偟傑偡丏
倁亖嚁(倓i亅倓bar)^2乛(n-1)
値亖僨乕僞偺屄悢 , 倃Ai亖俙孮偺僨乕僞 , 倃Bi亖俛孮偺僨乕僞
偙偙偱偺嵎偺暯嬒偲丆嵎偺暘嶶傪梡偄偰専掕摑寁検(倲0乯傪寁嶼偟傑偡丏
倲0亖乥倓bar乥乛(倁乛値)
嘍摑寁揑敾掕傪峴偆丏
乵椉懁専掕偺偲偒乶
倲0亙倲(n-1,兛) 側傜偼 丆乽婋尟棪100兛亾偱桳堄側嵎偑側偄乿
倲0亞倲(n-1,兛) 側傜偼 丆乽婋尟棪100兛亾偱桳堄側嵎偑偁傞乿
曅懁専掕偺偲偒乶
倲0亞倲(n-1,2兛)側傜偼 丆乽婋尟棪100兛亾偱戝偒偄乮彫偝偄乯乿
側偍,倲(n-1,兛)偼昞寁嶼僜僼僩乮僄僋僙儖丄娭悢幃乯偐傜媮傔傑偡丏
媮傔曽偼師偺乽椺戣22乿傪嶲峫偵偟偰壓偝偄丅
[椺戣22]
崅寣埑姵幰 10柤偵懳偡傞崀埑嵻偺搳梌慜偲屻偺寣埑抣傪師偵偵帵偟傑偡丏
搳梌屻偺寣埑偼搳梌慜傛傝桳堄偵掅偄偲塢偊傞偐偳偆偐傪専掕偟傑偡丏
| 搳梌慜 | 186 176 178 168 218 172 172 180 180 194 | |
| 搳梌屻 | 140 132 144 140 144 150 156 136 180 154 |
乮扨埵 mmHg乯
専掕偼師偺庤弴偱峴偄傑偡丏
嘆搳梌慜偲屻偺寣埑偺嵎(倓i)偲嵎偺俀忔(倓i^2乯偺寁嶼丏
| 慜 | 186 | 176 | 178 | 168 | 218 | 172 | 172 | 180 | 180 | 194 |
| 屻 | 140 | 132 | 144 | 140 | 144 | 150 | 156 | 136 | 180 | 154 |
| 倓i | 46 | 44 | 34 | 28 | 74 | 22 | 16 | 44 | 0 | 40 |
| 倓i^2 | 2116 | 1936 | 1156 | 784 | 5476 | 484 | 256 | 1936 | 0 | 1600 |
懳墳偡傞僨乕僞偺嵎(倓i)偺暯嬒(倓bar)偼師偺傛偆偵側傝傑偡丏
倓bar亖嚁倓i乛値亖 348乛10 亖34.8
懳墳偡傞僨乕僞偺嵎(倓i乯偺曃嵎暯曽榓(俽乯偲暘嶶(倁乯偼師偺傛偆偵側傝傑偡丏
俽亖嚁倓i^2亅乮嚁倓乯^2乛値亖15744亅348^2乛10亖3633.6 丂
倁亖俽乛(値亅侾)亖3633.6乛9亖403.733
埲忋偐傜丆専掕摑寁検(倲0乯偼丆
倲亖乥倓乥乛SQRT(倁乛値)亖34.8乛SQRT(403.733乛10) 亖5.477
偲側傝傑偡丏
専掕偼崀埑嵻偺搳梌偵傛偭偰丆寣埑偺掅壓偑摉慠梊憐偝傟傞偺偱曅懁専掕偲側傝傑偡丏
専掕偼丆
倲0亖5.477亜倲(9,0.1)亖1.833丂乮曅懁専掕丆婋尟棪5亾乯
偐傜丆搳梌慜傛傝傕搳梌屻偺寣埑偑桳堄偵掅偄偲塢偊傑偡丏
偡側傢偪丆崀埑嵻偺岠壥偑擣傔傜傟傞偲塢偊傑偡丏