- 乽僷儔儊僩儕僢僋専掕乿偼僨乕僞偑惓婯揑偱偁傞偲偒偵揔梡偡傞丏
- 乽僲儞僷儔儊僩儕僢僋専掕乿偼僨乕僞偑旕惓婯揑偱偁傞偲偒偲偐掕惈揑丒敿掕惈揑丒棧嶶検丆偁傞偄偼弴埵広搙偺僨乕僞側偳偵峀偔堦斒惈傪帩偨偣偰巊梡偱偒傞丏
- 乽摍暘嶶偺専掕乿偼乽5.2.1.乿偱愢柧偟偨丏
- 専掕摑寁検乮倲2乯偼乽僂僄儖僠専掕乿偲塢偄丆偦偺帺桼搙乮冇2乯偼巐屲擖偟偨惍悢抣傪梌偊傞丏
- 僨乕僞偺屄悢偑廫暘偵戝偒偄応崌偼暘嶶偺堎偄傪偁傑傝尩枾偵峫偊傞昁梫偼側偄丏偟偐偟柧傜偐側堎偄偑擣傔傜傟傞偲偒丆偦偺尷奅抣偼晄惓妋側悇掕抣偲側傞丏
- 婋尟棪傪 10亾掱傑偱崅偔偟偰摍暘嶶偺専掕傪峴偭偰傕椙偄丏壗屘側傜傟偼摍暘嶶偺寢壥傪尒偰偐傜杮専掕傪峴偆偐傜偱偁傞丏
- 堛妛偱偼姷廗揑偵倫亙0.05偺偲偒乽桳堄乿丆倫亙0.01偺偲偒乽旕忢偵桳堄乿偲塢偭偰偍傝丆乮*乯傑偨偼乮**乯傪晅偗偰昞尰偡傞偙偲傕偁傞丏
- 恾25偱偺倫抣偼倲暘晍昞偵偍偄偰丆偦偺桳堄悈弨乮兛乯偱帵偝傟傞倲暘晍偺僷乕僙儞僩揰埲壓偱桳堄偲塢偆堄枴偱偼側偄丏乵専掕偺庤弴乶偱帠慜偵寛傔偨桳堄悈弨乮兛乯傛傝倫抣偑彫偝偄偙偲傪堄枴偟偰偄傞丏
- 恾25偼侾場巕懡孮娫偱偺懡廳斾妑傪峴偭偨傕偺偱偼側偄丏偙傟偵偮偄偰偼乽侾尦攝抲暘嶶暘愅乮5.3.1乯乿偱愢柧偡傞丏
俀偮偺昗杮偺曣廤抍偵偍偗傞嵎偼丆乽暘晍偺僶儔僣僉偺嵎乿偱偁偭偰傕丆曣廤抍偱偺嵎傪悇應偝偣傑偡丏
梫偡傞偵僶儔僣僉偺堎偄偩偗傪栤戣偵偡傞側傜丆偙偙偱偺専掕偼昁梫側偄偱偟傚偆丏
偟偐偟丆堛妛傗堛妛偵娭楢偟偨暘栰偱偼丆偙偙偱偺乽暯嬒抣偺嵎偺専掕乿偑丆尋媶偺栚揑偵偐側偭偰偄傞応崌偑懡偄偺偱偡丏
偦偺傛偆側応崌丆専掕偼俀偮偺昗杮偺乽摍暘嶶惈乿偲乽惓婯惈乿偵傛偭偰丆偦偺庤朄傪堎偵偡傞偙偲傪抦傜側偗傟偽側傝傑偣傫丏
摍暘嶶惈偺壖掕偑媮傔傜傟傞棟桼偼丆堦曽偺昗杮偺暘嶶偑戝偒偔丆偁傞偄偼彫偝偔側傟偽偦偺暯嬒抣傕戝偒偔側偭偨傝丆彫偝偔側偭偨傝偡傞偐傜偱偡丏
傑偨丆惓婯惈傪慜採偲偡傞偙偙偱偺専掕偱丆堦曽偺暘晍偑榗傫偱偄傟偽丆暯嬒抣偵嵎偑弌傞偲摨帪偵丆偦偺暘嶶偵傕桳堄側嵎傪惗偠傞偙偲偑彮側偔偁傝傑偣傫丏
偦偺傛偆側偲偒偵偼丆揔摉側僨乕僞曄姺偵傛偭偰乽摍暘嶶惈乿偲乽惓婯惈乿偑惉傝棫偮傛偆偵偡傋偒偱偡丏
傕偟丆暯嬒抣偺嵎偩偗傪栤戣偵偡傞偺偱偁傟偽丆偐側傝惓婯暘晍偐傜棧傟偰偄側偄尷傝丆偙偙偱偺専掕傪梡偄偰傕椙偄偱偟傚偆丏
拲庍昞帵
偟偐偟丆惓婯惈偺壖掕偑嬌傔偰崲擄偱偁傞応崌偵偼丆愊嬌揑偵乽僲儞僷儔儊僩儕僢僋専掕乿傪梡偄傞傋偒偱偡丏 拲庍昞帵
摿偵丆弴埵広搙偺僨乕僞傗廫暘側悢偺僨乕僞偑摼傜傟側偄條側堛妛尋媶偱偼桳梡側摑寁庤朄偲側傝傑偡丏
傑偨丆偙偙偱偺専掕偼乽摍暘嶶惈乿偲乽俀偮偺昗杮偺娭楢惈乿偵傛偭偰丆偦偺専掕曽朄偑堎側傝傑偡偺偱廫暘偵拲堄偟偰壓偝偄丏
偡側傢偪丆乽俀偮偺昗杮偺娭楢惈乿偲偼丆
乽俙丏懳墳偺偁傞偲偒乿偲乽俛丏懳墳偺側偄偲偒乿
偱偁傝丆専掕偵偁偨偭偰偦偺慖戰傪岆傜側偄傛偆偵拲堄偟偰壓偝偄丏
俙丏懳墳偺側偄偲偒乮僷儔儊僩儕僢僋専掕乯丏
乽懳墳偺側偄偲偒乿偲偼丆俀慻偺堦曽偺僨乕僞偑崅偄傕偺偼懠曽偱傕崅偔丆掅偄傕偺偼懠曽偱傕掅偄偲塢偭偨摿掕偺孹岦偑尒傜傟側偄傕偺傪塢偄傑偡丏
偡側傢偪丆俀慻偺僨乕僞偑憡屳偵柍娭學側撈棫側懳徾偐傜偲傜傟偰偄傞傕偺偱偡丏
乵堦斒宍幃乶
乵専掕偺庤弴乶
1. 専掕偺栤戣傪柧偐偵偡傞丏
乽俀偮偺昗杮偺暯嬒抣偵嵎偑偁傞偐丠乿
2. 壖愢偺愝掕傪峴偆丏
婣柍壖愝乮俫0乯丗兪A亖兪B
懳棫壖愝乮俫1乯丗兪A亗兪B丂丂丂丂丂丂丂 乮椉懁専掕偺偲偒乯
懳棫壖愝乮俫1乯丗兪A亜兪B 傑偨偼 兪A亙兪B 乮曅懁専掕偺偲偒乯
3. 婋尟棪乮100兛亾乯傪愝掕偡傞丏
椉懁専掕偺桳堄悈弨丗兛 丂丂
曅懁専掕偺桳堄悈弨丗2兛
4. 専掕摑寁検乮倲1,倲2乯傪媮傔傞丏
摍暘嶶惈偺専掕乮5.2.1.嶲徠乯傪峴偭偰丆乽僶儔僣僉乿偑摍偟偄偲敾抐偝傟偨傜師偺乽専掕摑寁検乮倲1乯乿傪梡偄傑偡丏
倲1亖ABS(嘳barA亅嘳barB乥乛 SQRT乮k(1/nA亄1乛nB)
K亖乮nA-1乯VA亄乮nB亅1乯VB 乛(nA亄nB亅2)
摍暘嶶惈偺専掕傪傪峴偭偰丆乽僶儔僣僉乿偑堎側傞偲敾抐偝傟偨傜丆師偺乽専掕摑寁検乮倲2乯乿傪梡偄傑偡. 拲庍昞帵
倲2亖ABS(嘳A亅嘳B)乛SQRT(VA乛nA亄VB乛nB )
値A亖俙孮偺僨乕僞偺屄悢 , 値B亖俛孮偺僨乕僞偺屄悢
嘳barA亖俙孮偺暯嬒抣 , 嘳barB亖俛孮偺暯嬒抣
倁A亖俙孮偺暘嶶 , 倁B亖俛孮偺暘嶶
5. 摑寁揑敾掕傪峴偆丏
乵椉懁専掕偺偲偒乶
倲1亙倲(冇,兛) 傑偨偼 倲2亙倲(冇,兛) 側傜偽丆乽婋尟棪100兛亾偱桳堄側嵎偑側偄乿
倲1亞倲(冇,兛) 傑偨偼 倲2亞倲(冇,兛) 側傜偽丆乽婋尟棪100兛亾偱桳堄側嵎偑偁傞乿
乵曅懁専掕偺偲偒乶
倲1亞倲(冇,2兛 ) 傑偨偼 倲2亞倲(冇,2兛 ) 側傜偽丆 乽婋尟棪100兛亾偱戝偒偄乮彫偝偄乯乿
偙偙偱丄倲(冇,兛)偼倲暘晍昞乽昞寁嶼僜僼僩乮僄僋僙儖乯乿偐傜媮傔傑偡丏媮傔曽偼乽椺戣20乿傪嶲峫偵偟偰壓偝偄.
側偍丆専掕摑寁検乮倲1乯偺偲偒偺帺桼搙偼丆
冇1亖値A亄値B亅2
専掕摑寁検乮倲2乯偺偲偒偺帺桼搙偼丆 拲庍昞帵
冇2亖 1乛乷C^2乛(nA-1)亄(1亅C)^2乛乮nB亅1乯}
偙偙偱丆
C亖(VA乛nA)乛(VA乛nA亄VB乛nB)
偐傜媮傔傑偡丏
6. 100乮1亅兛乯亾怣棅尷奅傪媮傔傞丏
俀孮偺僨乕僞偺暘嶶偑摍偟偄偲偒偺丆100乮1亅兛乯亾怣棅尷奅偼師偵傛傝媮傔傑偡丏
拲庍昞帵
忋尷抣丗
ABS(嘳A亅嘳B)亄倲(冇1 ,兛)亊SQRT(K(1/nA亄1/nB))
壓尷抣丗
ABS(嘳A亅嘳B)亅倲(冇1 ,兛)亊SQRT(K(1/nA亄1/nB))
乽椺戣20乿
偙偙偱偼暯嬒抣偵嵎偑偁傞偐傪栤戣偵偟偰傒傑偟傚偆丏僨乕僞偼師偺捠傝偱偡丅
(A)擭楊 30乣39嵥, 30柤偺暯嬒抣倃barA亖122.5 mmHg, 昗弨曃嵎倱A亖 10.85 mmHg
(B)擭楊 40乣49嵥, 20柤偺暯嬒抣倃barB亖133.4 mmHg, 昗弨曃嵎倱B亖 12.24 mmHg
(C)擭楊 50嵥乣乣 , 10柤偺暯嬒抣倃barC亖139.0 mmHg, 昗弨曃嵎倱C亖 20.4 mmHg
嵟弶偵丆暘嶶斾偺専掕傪峴偄傑偡丏乮5.2.1.嶲徠乯
1. 昗杮乮俙丗30嵥戙乯偲昗杮乮俛丗40嵥戙乯偺専掕丏
昗杮偺暘嶶偲僨乕僞偺屄悢偼丆
倁A亖117.72丆倁B亖149.82 丆値A亖30丆値B亖20丂
丂丂
偱偁傞偺偱 丆
俥2亖倁B乛倁A丂偼師偺捠傝偱偡丏
俥2亖149.82乛117.72亖1.273
1.273亙俥(nB-1,nA-1, 0.1乛2)亖 2.168
俥(nB-1,nA-1, 0.1乛2) 偼乽昞寁嶼僜僼僩乮僄僋僙儖乯偐傜媮傔傑偡乿.
偟偨偑偭偰丆
婋尟棪10亾偱桳堄側嵎偑側偄偺偱丆摍暘嶶偲塢偊傞偱偟傚偆丏
拲庍昞帵
2. 昗杮乮俛丗40嵥戙乯偲昗杮乮俠丗50嵥戜戙乯偺専掕丏
昗杮偺暘嶶偲僨乕僞偺屄悢偼丆
VB亖149.82 丆VC亖416.16
値B亖20 丆値C亖10丂
丂丂
偱偁傞偺偱丆
俥2亖VC乛VB丂偼師偺捠傝偱偡丏
俥2亖416.16乛149.82亖2.778
2.778亜俥(nC-1,nB-1, 0.1乛2)亖2.423
偟偨偑偭偰丆
婋尟棪10亾偱桳堄側嵎偑偁傞偲塢偊傞偺偱丆摍暘嶶偲塢偊側偄偱偟傚偆丏
埲忋偐傜丆
昗杮乮俙丂丂丂丂乯偲昗杮乮俛乯偼乽倲専掕 乿
昗杮乮俙傑偨偼俛乯偲昗杮乮俠乯偼乽僂僄儖僠専掕乿
傪揔梡偟傑偡丏
師偵杮専掕偱偁傞乽暯嬒抣偺嵎偺専掕乿傪峴偄傑偡丏
1. 昗杮乮俙乯偲昗杮乮俛乯偺専掕丏
昗杮偺暯嬒抣偲暘嶶偼丆
嘳A亖122.5 丆嘳B亖133.4丆倁A亖117.72丆倁B亖149.82丂偱偁傞偺偱丆専掕摑寁検乮倲1乯偼師偺傛偆偵側傝傑偡丏
倠亖{ (nA亅1)VA亄(nB亅1)VB }乛(nA亄nB亅2)亖 (29亊117.72 亄 19亊149.82)乛(30亄20亅2)
K亖130.43
倲1亖ABS(嘳A乗嘳B)乛SQRT(k亊(1乛nA亄1乛nB))亖ABS(122.5-133.4)乛(130.43亊(1乛30亄1乛20))
偁傞偺偱丆
倲1亖3.306亜倲(冇1 , 0.05乯亖2.011 乮椉懁専掕丆婋尟棪 5亾乯
冇1=30亄20亅2
偐傜丆桳堄側嵎偑偁傞偲塢偊傑偡丏
偙偙偱偺暯嬒抣偺嵎偺 95亾怣棅尷奅偼丆
嘳A亅嘳B亇倲(冇1,兛)亊 SQRT(k亊(1乛nA+1乛nB)
亖122.5亅133.4亇倲(48 , 0.05乯亊SQRT(10.869)
亖-10.9亇2.011亊3.297亖-10.9亇6.63
偟偨偑偭偰丆昗杮乮俙乯偲昗杮乮俛乯偺寣埑偺僇僞儓儕偼 -17.53 乣 -4.27mmHg 偺斖埻撪偺抣偲悇掕偝傟傑偡丏
2. 昗杮乮俙乯偲昗杮乮俠乯偺専掕丏
摍暘嶶偲塢偊側偄偺偱乽僂僄儖僠偺専掕乿傪峴偄傑偡丏
昗杮偺暯嬒抣偲暘嶶偼丆
嘳A亖122.5 丆嘳C亖139.0
VA亖117.72 丆VC亖416.16丂
偱偁傞偺偱丆 丂丂
専掕摑寁検乮t2乯偼師偺傛偆偵側傝傑偡丏
t2亖ABS(嘳A-嘳C)乛SQRT(VA乛nA亄VC乛nC)亖ABS(122.5-139.0)乛SQRT(117.72乛30亄416.16乛10)
亖 2.445 丂
偟偨偑偭偰丆
倲2亖2.445亜倲(冇2,0.05)亖2.201 乮椉懁専掕丆婋尟棪 5亾乯
冇2亖11丂丂
偐傜丆桳堄側嵎偑偁傞偲塢偊傑偡丏
側偍丆偙偙偱偺倲暘晍偺僷乕僙儞僩揰傪梌偊傞帺桼搙乮冇2乯偼師偵傛傝媮傔傑偡丏
C亖(VA乛nA)乛( VA乛nA亄VC乛nC)亖 117.72/30乛(117.72乛30 亄 416.16乛10)亖0.086
冇2亖1乛(C/nA亄(1-C)/nC)亖1乛(0.086乛29亄0.914乛9)亖10.77亗11
3. 昗杮乮俛乯偲昗杮乮俠乯偺専掕丏
摍暘嶶偲塢偊側偄偺偱乽僂僄儖僠偺専掕乿傪峴偄傑偡丏
昗杮偺暯嬒抣偲暘嶶偼丆
嘳B亖133.4 丆嘳C亖139.0
VB亖149.82 丆VC亖416.16丂
偱偁傞偺偱丆 丂丂
専掕摑寁検乮t2乯偼師偺傛偆偵側傝傑偡丏
専掕偼乽2.乿偲摨條偵偟偰丆
t2亖0.799亙t(冇2 , 0.05乯亖 2.179 乮椉懁専掕丆婋尟棪 5亾乯
偐傜丆桳堄側嵎偑側偄偲塢偊傑偡丏側偍帺桼搙乮冇2乯偼乽2.乿偲摨偠傛偆偵寁嶼偟傑偡丅
師偺傛偆偵側傝傑偡丏
冇2亖1乛(0.153^2乛19亄0.847^2乛9) 亖12.3512 亗 12
埲忋乽1.乿乽2.乿乽3.乿偺専掕寢壥偼恾25偺條偵昞偡偙偲傕弌棃傑偡丏
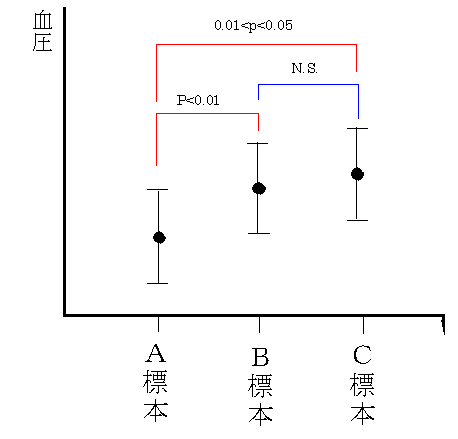
恾25偼俁昗杮娫偺暯嬒抣偺専掕寢壥傪昞傢偡堦曽朄偱偁傞.
乽N.S.乿(Non-Signification)偼桳堄嵎側偟傪昞傢偡.