- Chochran法の他に,Mantel-Haenszel法とOdds法などがある。
- これについては、表計算ソフト「エクセル」の「sheet(M-H)」及び「Odds」を参考にされたい。
C.対応のあるとき.
m×2分割表が2組あって,2組の出現率の差を検定したいときに用います.
ここでは,2組の全体的な出現率の差が均等であるかどうかなどを検定する手法を示します.
[一般形式]
| 水準 | A群 | B群 | ||
|---|---|---|---|---|
| (A) | 標本数 | 出現率 | 標本数 | 出現率 |
| A1 | n11 | p11 | n12 | p12 |
| A2 | n21 | p21 | n22 | p22 |
| : | : | : | : | : |
| Ai | ni1 | pi1 | ni2 | pi2 |
| : | : | : | : | : |
| Am | nm1 | pm1 | nm2 | pm2 |
[検定の手順]
1. 検定の問題を明かにする.
「 A群とB群の出現率に差があるか? 」
「 その差は均等であるか ? 」
2. 仮設の設定を行う.
帰無仮設(H0):PA=PB
対立仮設(H1):PA≠PB
3. 危険率(100α%)を設定する.
両側検定における有意水準:α
4. 検定統計量(KAI)を計算する。
表19 の計算表にもとづいて計算します.
| 要因 | ⊿pi | pibar | qibar | di | ni1 | ni2 | ni. | wi | wid1 | widi^2 |
| A1 | ⊿p1 | p1bar | q1bar | d1 | n11 | n12 | n1. | w1 | w1d1 | w1d1^2 |
| A2 | ⊿p2 | p2bar | q2bar | d2 | n21 | n22 | n2. | w2 | w2d2 | w2d2^2 |
| : | : | : | : | : | : | : | : | : | : | : |
| Ai | ⊿pi | pibar | qibar | di | ni1 | ni2 | ni. | wi | widi | widi^2 |
| : | : | : | : | : | : | : | : | : | : | : |
| Am | ⊿pm | pmbar | qmbar | dm | nm1 | nm2 | nm. | wm | wmdm | wmdm^2 |
| 計 | - | - | - | - | - | - | - | Σwi | Σwidi | Σwidi^2 |
ここで,
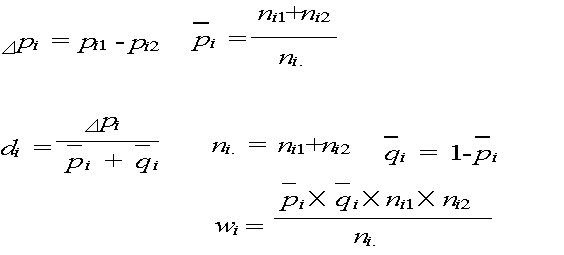
表19 の計算表から,以下の各検定統計量(Chochran 法)を求めます.
全体の検定統計量(KAIt2)は,
KAIt=∑wi・di2
均等性の検定統計量(KAIh2)は,
KAIh2=∑wi・di-(wi・di)/∑wi
となります.
5. 統計的判定を行う.
KAIt2<KAI2(m,α)ならば,「 危険率100α%で出現率に差がない 」
KAIt2≧KAI2(m,α)ならば,「 危険率100α%で出現率に差がある 」
ここでの検定はm群全体に共通しているものか,どうか分かりませんので,水準間でその差の程度が異なるか,どうかを次により判定します.
KAIh2<KAI2(m-1,α)ならば,「危険率100α%で出現率は均等である」
KAIh2≧KAI2(m-1,α)ならば,「危険率100α%で出現率は均等でない」
なお,KAI2(m,α),KAI2(m-1,α),KAI2(1,α)は KAI分布表(表計算ソフト「エクセル」)から求めます.求め方は「例題」を参考にして下さい.
[ 例題 13 ]
心電図検査における精度管理において表20 の結果を得ました.年齢ごとの要精密検査者数(要精検者数)の割合は,男性と女性で差があるか検討してみましょう.
| 年齢 | 男性 | 女性 | ||||
|---|---|---|---|---|---|---|
| (才) | 実施者数 | 精検者数 | 精検率 | 実施者数 | 精検者数 | 精検率 |
| ~39 | 53 | 4 | 0.075 | 8 | 1 | 0.125 |
| 40~49 | 186 | 9 | 0.048 | 91 | 2 | 0.022 |
| 50~59 | 138 | 11 | 0.080 | 31 | 1 | 0.032 |
| 60~69 | 39 | 7 | 0.179 | 8 | 1 | 0.125 |
| 70~ | 4 | 2 | 0.500 | 6 | 1 | 0.167 |
検定は表19 の計算表にもとづき検定統計量を求めます.ここでは表計算ソフト「エクセル」での方法を示します.
表計算ソフト「エクセル」の結果から、Cochran の方法では、
検定統計量(KAIt2,KAIh2)は,
KAIt2 = 3.618
KAIh2 = 1.423
となる。よって、
KAIt2 = 3.618<KAI(5,0.05) = 11.070
であり、危険率5%で全体的に男性と女性の精検率に差があると言えません。そして、
KAIh2 = 1.423<KAI2(4,0.05) = 9.488
から、危険率5%で精検率は、全体的に年齢区分と関連性があり、均等と言えるでしょう。
もし、KAIh2≧KAI2(4,0.05)ならば、均等とは言えないので、年齢区分を再検討すべきでしょう。
KAIa2 = 2.194<KAI2(1,0.05) = 3.841
から、危険率5%で両群での精検率の差は「0」に近いと言える。