戻る　　　　　次へ　　　　　目次へ

3.2. 両側検定と片側検定について．
検定において「有意」とは帰無仮説（Ｈ₀）を棄却し，対立仮説（Ｈ₁）を採用することでした． Ｈ₁の採用は単に「有意な差」だけを検定での問題にしているのでしょうか．
あるいは，いずれか一方の平均値（Ｘ^-）と比較したとき，他方の平均値（Ｙ^-）に比べてＸ^-＞Ｙ^-なのか，
あるいはＸ^-＜Ｙ^-なのかを検定の問題にしているのか考えなければなりません．

先の血圧の例(3.1.1.)では1000名の母平均（ μ ）と２０名の標本の平均（Ｘ^-）との間に有意な差があるかどうかが問題でした．
したがって，検定の仮説はＸ^-＝μ の帰無仮説（Ｈ₀）に対して，Ｘ^-≠ μ を対立仮説（Ｈ₁）としたのです．
もし，２０名の平均値（Ｘ^-）が1000名の母平均（ μ ）よりも 明らかに大きいか，
あるいは小さいと予想されるならば， 対立仮説（Ｈ₁）はＸ^-＞ μ ，またはＸ^-＜ μ とすべきでしょう．

もしＸ^-＝ μ について検定をおこなうなら，
それは図23 のようにＮ（1,σ²）の分布の両側に有意水準（ α ）の 1／2の限界点を設けたことになります．
これを両側危険域と云いその検定を両側検定と云います．

これに対しＸ^-＞ μ ，Ｘ^-＜ μ について検定をおこなうなら，
Ｎ（1,σ²）の分布の片側に有意水準（ α ）の限界点を設けたことになり，これを片側危険域と云いその検定を片側検定と云います．

図23 のように両側と片側では同じ危険率でもその有意水準の異なることに注意しなければなりません．

図23　両側危険域と片側危険域における有意水準

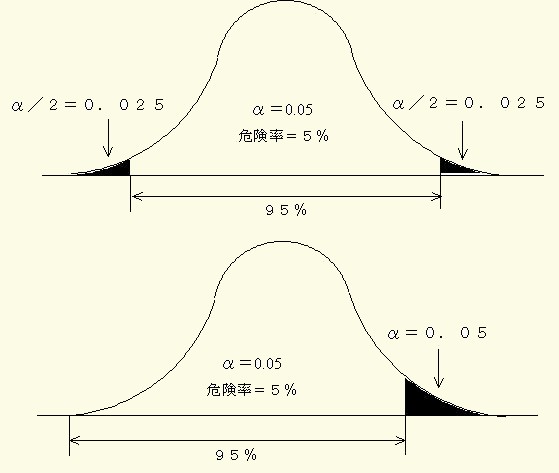
先の血圧の例では次のようになります．

有意水準を α ＝0.05（危険率５％）としたとき，

両側検定（Ｈ₁：Ｘ^-≠ μ ） では，
Ｚ₀＝0.65 ＜Ｚ（ α ＝0.05／2）＝1.96

から，危険率５％で有意な差はないと云えます．

なお、1.96は表計算ソフト「エクセル」から求めた α ＝0.025 に対応するパーセント点である． 注釈表示

「1.96」，「1.64」の限界点は標準正規分布のパーセント点であり，これは表計算ソフト「エクセル」から求める． 求め方などは５章以降を参照されたい．

パーセント点は，関数式[＝NORMSINV(0.025)] より求められる．

片側検定（Ｈ₁：Ｘ^-＞ μ または Ｘ^-＜ μ ）では，　

Ｚ₀＝0.65 ＜Ｚ( α ＝0.05 )＝1.64

から，危険率５％でＨ₀を採択できます． すなわち，Ｘ^-＞ μ または Ｘ^-＜ μ ではないと云えます ．

なお、1.64 は表計算ソフト「エクセル」から求めた α ＝0.05 に対応する パーセント点 である．

パーセント点は，関数式[＝NORMSINV(0.05)] より求められる．

この様に危険率が同じであっても片側検定は両側検定よりも有意になるので，両側か片側か， その選択を迷うときには，対立仮説（Ｈ₁）をＸ^-≠μとすると良いでしょう．
そしてＨ₁が採用されれば，それはＸ^-＞ μ かあるいは ，Ｘ^- μ のどちらかです．

3.3. 推定の問題について．
Ｎ（ μ , σ ² ）の正規母集団からとられた標本の平均値（Ｘ^-）の分布が， しだいにＮ（μ , σ ／SQRT(n)）の分布になることはすでに説明したとおりです．

また，標本の平均値（Ｘ-）は母平均 μ を中心に Ｘ^- ± 1.96 σ ／SQRT( X )の範囲に 95％ ，Ｘ^-±2.58 σ ／SQRT( n ) の範囲に 99％ の確率で入り ， この範囲外に出る確率は 5 ％と 1 ％ に過ぎないことが分かります．
したがって，この範囲内に母平均（ μ ）が含まれる割合は 95％ と 99％です．これを信頼限界と云いその範囲を信頼区間と云います．

例えば、次の血圧値「データの個数 ｎ＝20 ,平均値（Ｘ^-）＝ 133.8 mmHg」を例にとると，

[ 118,148,128,141,139,120,125,123,134,144,138,134,126,138,116,130,154,161,132,126 ]mmHg

母平均 μ の 95％ 信頼限界の推定値は，

Ｘ^-±1.96 σ ／SQRT( n )＝133.8 ± 1.96×19.2／SQRT(20)＝ 125.4 〜 142.2 mmHg

99％信頼限界は，

Ｘ^-±2.58 σ ／SQRT( n )＝133.8 ± 2.58×19.2／SQRT(20)＝ 122.7 〜 144.9 mmHg

となります．

母集団（1000 名）の母平均値（ μ ）は ，131 mmHg ですので，この値は信頼率 95％の信頼区間に入っており， 先の検定結果と一致します．

ここでの血圧値の例では，母集団での標準偏差が既知（ 19.2 mmHg ）でした． 実際には ，σ が未知のことが多く，標本での標準偏差（ｓ）を用いて推定することになります．

標本での標準偏差（ｓ）を用いるときは ｔ分布のパーセント点を使用します． その計算方法などは４章以降で説明します．

ここでの「検定の問題」と「推定の問題」では，１標本のときについて説明したが，この考え方は２標本の時でも同じです．

２標本での検定や推定においては，２つの平均値をＸ^-，Ｙ^-とするとき， その平均値の差「ｄ＝Ｘ^-−Ｙ^-」を標準化した値が，特定の値であるかどうかをＮ（0,1²）の分布について考えれば良いのです．

3.4. 異常値の棄却．
正規分布またはデータ変換後の正規分布近似において，その分布から１つだけ極端にはなれたデータがあるとき， これを勝手に除外せず，「棄却検定」を行ってから判断しなければなりません．
ここでは一般的な「グラブス・スミルノフの棄却検定」について説明します．

［一般形式］

検定は次の手順で行います．

［検定の手順］
１） 検定の問題を明らかにする．
「飛び離れたデータ（値）は棄却できるか？」

２） 仮設の設定を行う．
帰無仮説（Ｈ₀）：棄却できない．
対立仮説（Ｈ₁）：棄却できる．

３）危険率を設定する．
検定の問題によって異なるが，通常 , α＝ 0.01（危険率１％）または ， α＝ 0.05（危険率５％）である．

４）検定統計量（Ｔ₀）を計算する．
Ｔ₀＝（Ｘ₀−Ｘ^-）／ｓ

ここで，Ｘ₀＝飛び離れた値，Ｘ^-＝平均値，ｓ＝標準偏差　である．

５）統計的判定を行う．
Ｔ₀＜Ｔ_n（ α ）ならば，「 危険率100α ％ で棄却できない」．
Ｔ₀≧Ｔ_n（ α ）ならば，「 危険率100α ％で 棄却できる　」．

なお，Ｔn（ α ）は次式より求める．

Tn(α)＝

(n-1) × t(n-2,α/n) n(n-2)＋ n × t(n-2,α/n)^2

但し，ｎ＝データの個数である．なお、t( n-2 , α/n ) は ｔ分布表（ 表計算ソフト「エクセル」）から求めることができる．

［例題８］
成人健常者 50 名の血中免疫グロブリン（ＩgＭ； 単位 mg/dl）のデータを表 12 に示します．このうち，500 mg/dl を異常値として棄却できるでしょうか検定してみましょう．

ＩgＭのヒストグラムは図 24-1（変換前）のように，右すそ型の分布を示すので ， Ｘ^(1/3)変換（Ｘ^(1/2) 変換 ，ルート変換でも良い）を行い正規分布に近づけてから棄却検定を行います． 注釈表示

棄却検定は正規分布または正規分布に変換したデータについて行う．

２つ以上の飛び離れたデータがあるときは「有意」，すなわち「棄却」できにくくなる

検定で「有意（棄却）」の結果を得たとき，その原因を探求せずにデータを除去すべきでない.

変換後のデータを表13 に，変換前後のヒストグラムを図24-2に示します．

表12　免疫グロブリン（ＩgＭ）の血中濃度
「変換前のデータ（mg／dl）」

---

114,214,140,140,500, 54, 94,100, 93,124
105,162,124, 77,162,104,204,124, 54,110
226,214, 86,111,124,248,214,204,171,108
95,124,182,162, 92,108, 77,236, 98, 77
130,100,124,140,104,162, 54,140, 60,204

---

表13　免疫グロブリン（ＩgＭ）の血中濃度
「変換後のデータ（Ｘ^(1/3)の値）」

---

4.58,5.98,5.19,5.19,7.94,3.78,4.55,4.64,4.53,4.99
4.72,5.45,4.99,4.25,5.45,4.70,5.89,4.99,3.78,4.79
6.09,5.98,4.41,4.81,4.99,6.28,5.98,5.88,5.55,4.76
4.56,4.99,5.67,5.45,4.51,4.76,4.25,6.18,4.61,4.25
5.07,4.64,4.99,5.19,4.70,5.45,3.78,5.19,3.91,5.89

---

図24-1　ＩgＭ値の変換前のヒストグラム

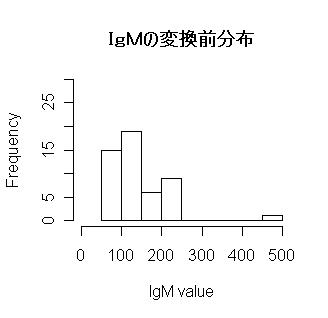
図24-2 変換後（Ｘ^(1/3)）のヒストグラム

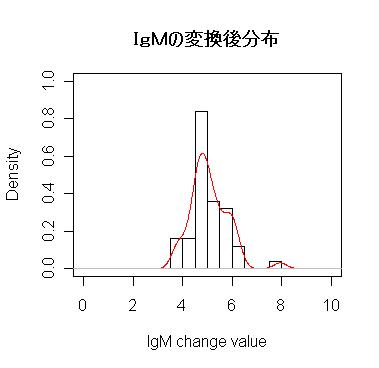
棄却検定の計算は次の通りです．
棄却対象のデータ（Ｘ₀）＝7.94 ，全データの平均値（Ｘ^-）＝5.068 ，全データの標準偏差（ｓ）＝0.762　ですので，
その検定統計量（Ｔ₀）は，

Ｔ₀＝(7.94−5.068)/ 0.762＝ 3.769

となります．
なお，ｔ₅₀（α）はｔ（α/n,n-2）＝ｔ（0.0002,48）＝4.027 ですので，Ｔ₅₀（0.01）＝3.482　となります．

表計算ソフト「エクセル」では，「=TINV(0.0002,48)」で求めることができます．

したがって，

Ｔ₀＝3.769 ＞Ｔ₅₀（0.01）＝3.482 から，「危険率１％でこのデータは棄却できる」 と判断されます．

戻る　　　　　次へ　　　　　目次へ　　　　　TOPへ