- 医学での実験において分析誤差を表現するとき,標準偏差(s)や変動係数(CV)を用いて,
同時再現性や日差再現性などの精密度を表すことがある.
この時,正規分布でないデータでは中央値(Me)や,四分位偏差(QR)で表現する方が良い場合もある. - 医学実験でのバラツキには,(a)実験方法や実験器具の誤差によるもの,(b)実験者の手技誤差によるもの,(c)実験での偶発的あるいは系統的な誤差によるもの,などがあり,これらの評価に標準偏差(s)や変動係数(CV)が役立つ.
- 医学での研究発表や論文において,データの分布やバラツキの程度を箱ひげ図」で示すことがある.基本的な「箱ひげ図」(図15,16)の構成を示しておく.
戻る 次へ 目次へ
2.3.統計量の計算の仕方.
収集したデータを度数分布に整理し,データの分布を把握したのちにデータの性質を記述します.通常,記述はデータの分布の代表値とバラツキで表現するの良いでしょう.
データが度数分布で与えられているような離散量であっても同じです.
2.3.1. 連続量からの計算.
データをそのまま使用して,代表値(平均値など)や分散(バラツキ)などを計算します.
代表値には次の「一般形式」のように示すように,平均値・中央値・最頻値があります.
[代表値の一般形式]
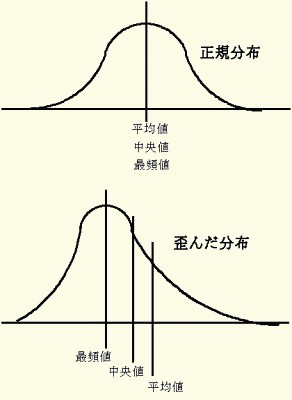
正規分布での代表値(平均値・中央値・最頻値)は同じ値であるけれども,歪んだ分布での代表値は,それぞれ異なっていることがあります.
[生データからの計算手順]
表5によってデータの集計をおこなうと便利です.
| 番号 | データ | データの2乗 |
|---|---|---|
| 1 | X1 | X1^2 |
| 2 | X2 | X2^2 |
| . | . | . |
| i | Xi | Xi^2 |
| . | . | . |
| n | Xn | Xn^2 |
| 合計 | ∑Xi | ∑Xi^2 |
そして,表5の計算表から次の各統計量を計算します
1. 分布の中心を表す統計量
平均値(X-)
X-=∑Xi/n
中央値(Me):データを大きさの順に並べます.すなちわデータを順位系列(X1<X2<・・・<Xn)として次式より求めます.
nが奇数のとき;Me=Xn+1/2;(データの個数+1)/2番目
nが偶数のとき;Me=(Xn/2+Xn/2+1)/2;{(データの個数/2)番目+(データの個数/2+1)}/2番目
最頻値(M0):最頻値とは,度数分布において最も度数の大きな階級に位置する値であり,その値は(2.3.2.[度数分布からの計算手順])から求める方が良いでしょう.
2. 分布のバラツキを表す統計量
分散(V)と標準偏差(s)
偏差平方和(S)=∑(Xi-X-)^2=∑Xi^2-(∑Xi)^2/n
分 散 (V)=S/(n-1)
標準偏差(s)= SQRT(V)
標準誤差(SE)=s/SQRT(n)
(SE)については3章(3.1.)で説明します.(3.1.)
四分位偏差(QR);データを大きさの順に並べ,順位系列(X1<X2<・・・<Xn)を作ります.そしてデータ全体を4等分したとき,その中央値(Me)を第2四分位数と云います.
また,その下半分の1/2を第1四分位数(Q1),上半分を第3四分位数(Q3)と云います.
したがって,QR=Q3-Q1を四分位偏差と云い,全データの1/2が含まれます.
データの数が多いときは,(2.3.2[度数分布からの計算手順])から求める方が便利でしょう.
変動係数(CV);データの大きさや単位に関係なく各データ間の分布のバラツキなどを示すのに用います.
CV=標準偏差(s)/X-
分布の形状を表す統計量
歪度(m3);平均値を中心とする分布の非対称性の方向とその程度を表します.左右対称な分布ではm3=0,右すそ型ではm3>0 ,左すそ型ではm3<0 となります.
歪度(m3)は次式で求めます.
m3=1/n・∑(Xi-X-)^3/s^3
尖 度(m4);平均値まわりのデータの集中度を表します.正規分布ではm4=3になります.尖度(m4)は次式で求めます.
m4=1/n・∑(Xi-X-)^4/s^4
[例題5]
健常成人50名の血糖測定値
(例題1[表1])
を用いて,基本的な統計量を計算してみましょう.
表計算ソフト「エクセル」による結果を示します。
● 関数式による方法
次に,四分位偏差(QR)は,データを小さい方から大きさの順に並べた昇順順位系列から求めるます.
すなわち,中央値(メジアン)=89,第1および第3四分位数は中央値との1/2であるからQ1=86,Q3=96,したがって四分位差は QR=Q3-Q1=96-86=10です
● 関数式による方法
これらの代表値とバラツキは,医学において図15 のように表わされることがあります.
図15 代表値とバラツキの箱ひげ図の一例
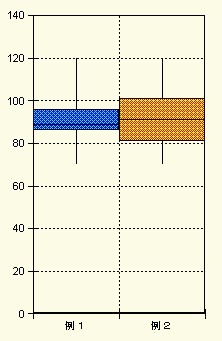
図説では代表値とバラツキが中央値と四分位数(例1)なのか,平均値と標準偏差(例2)なのかを明確にすべきです.
● バラツキを標準偏差で示す場合の条件として、
平均値>標準偏差×2(2SD)
を目安にして下さい。
それ以外のときは、積極的にパーセントタイルを用いて要約することを勧めます。
なお,ここでの血糖値の分布の形状を表わす,
歪度(skewness:m3)は m3=0.668
尖度(kurtosis:m4)は m4=0.813
であり,これは正規分布に近似した右すそ型を表わしています.すなわち、
m3>0 であれば、右すそ広がりの分布.
m3=0 であれば、正規分布.
m3<0 であれば、左すそ広がりの分布.
m4>0 であれば、すそ広がりが強い.
m4=0 であれば、正規分布.
m4<0 であれば、すその広がりが少ない分布.
と見ることができる.
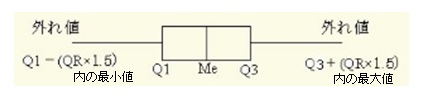
図16 外れ値を示す箱ひげ図
2.3.2 離散量からの計算.
度数分布から平均値や分散などを計算します.
[代表値の一般形式]
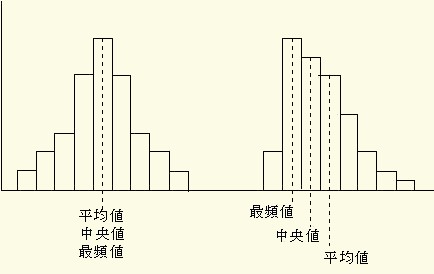
度数分布で与えられたようなデータであっても,その分布が正規分布であれば代表値(平均値・中央値・最頻値)は同じ値をとります.しかし,歪んだ分布ではそれぞれ異なる値をとることがあります.
[度数分布からの計算手順]
表6によりデータの集計を行ないます.
| 変量 | 度数 | 級和 | 2乗和 |
|---|---|---|---|
| X1 | f1 | f1・X1 | f1・X1^2 |
| X2 | f2 | f2・X2 | f2・X2^2 |
| ・ | ・ | ・ | ・ |
| Xi | fi | fi・Xi | fi・Xi^2 |
| ・ | ・ | ・ | ・ |
| Xk | fk | fk・Xk | fk・Xk^2 |
| 合計 | ∑fi | ∑fi・Xi | ∑fi・Xi^2 |
[分布の中心を表す統計量]
1.平均値(X-):X-=(∑f・Xi)/n
2.中央値(Me):度数分布表からグラフ用紙に相対累積度数分布線を描き,その50 %点に一致する変量値,
>
または級代表値が目盛られた軸上の値を求めます.「例題6」を参考にして下さい.
3.最頻値(MO):度数分布表から,
最大度数を持つ階級の下限値=Lm
その次の階級の度数 =fm+1
その前後の階級の度数の合計=fm-1 +fm+1
級間(級の幅)=h
を求め,次式により計算します.
|
|
[分布のバラツキを表す統計量]
1.分散(V)と標準偏差(s)
2.偏差平方和(S):S=∑fi・Xi^2-(∑fi・Xi)^2/n
3.分散(V):V=S/(n-1)
4.標準偏差(s):s=SQRT(V)
5.四分位偏差(QR):度数分布表からグラフ用紙に相対累積度数分布線を描き,その25%と75%点に一致する変量値,または級代表値が目盛られた軸上の値から,それぞれ第1四分位数(Q1)と第3四分位数(Q3)を求めます.四分位偏差は,QR=Q3-Q1です.
次の「例題6」を参考にして下さい
[分布の形状を表す統計量]
1.四分位歪度:{(Q3-Q2)-(Q2-Q1)}/(Q3-Q1)
2.分位尖度 :(Q3-Q1)/(D9-D1)
ここで、「D9,D1」は10%点と90%点に当たる。
[例題6]
健常成人50名の血糖測定値の度数分布
(例題1[表1])
を用いて,基本的な統計量を計算してみましょう.
また,
次に示す図17の相対累積度数曲線から,四分位数などを求めてみましょう。
図17 度数分布から求めた相対累積度数曲線
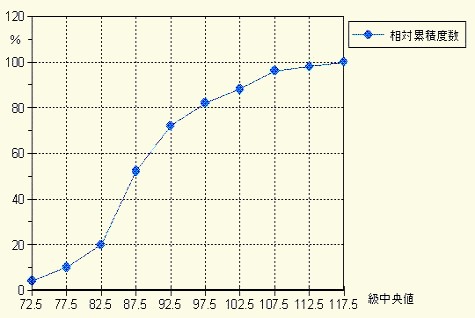
以下の計算は「分析ツールによる方法」(例題6-2)を参考にして下さい。
第1四分位数(Q1)は25%点のQ1=86.5
第24分位数(Q2)は50%点のQ2=90.5
第3四分位数(Q3)は75%点のQ3=96
となります.したがって,
四分位偏差(QR)はQR=Q3-Q1=10.5 となります.
なお,
最頻値は(Mo)は,
Lm=85
fm+1=10
(fm-1+fm+1)=5+10=15
h=5
から,
Mo=85+10×5/15=88.33
を得ます.
また,ここでの
四分位歪度は {(96-90.5)-(90.5-86.5)}/(96-86.5)=0.158
分位尖度は D1=80.8 , D9=107 ですので、(96-86.5)/(107-80.8)=0.363
となります。
四分位歪度は、正に歪んでいるときは「正の値」を、負に歪んでいるときは「負の値」となります。これは連続量のときと同じです。
分位尖度は尖りが大きくなるほど小さい値となり、正規分布では0.56となっています。これは連続量のときと逆です。
これらの値は,生データから計算した値と異なっている点に注意して下さい.より正確には,度数分布の級数を多くして計算すれば良いでしょう.
2.3.3. 平均値・分散の結合.
2組以上の関連する標本について,その大きさと平均値および,標準偏差が分かっているとき,それらを一つにしたいときがあります.この様なときの平均値と標準偏差の求め方を説明しましょう.
[結合の一般形式]
[結合の計算手順]
k組の標本の大きさがni(i=1,2,・・・,k)で, その平均値がXi-,標準偏差がsiであるとき,k組を一つにした標本の大きさ(データの個数n)は,
n=∑ni
であるから,
その合計値(T)と,平均値(X-)は,
T=∑Ti ,Ti=mi×ni ,X-=T/n
です.したがって,
その偏差平方和(S)は,
S=∑Si+∑ni(Xi-X-),Si=si2(ni-1)
によって求めることができます.よって,
その分散(V)と標準偏差(s)は
V=S/(n-1),
s=SQRT(V)
となります.次の「例題7」を参考にして下さい.
[例題7]
Aの標本(データの個数nA=20,平均値XA-=89.75, 標準偏差sA=6.463)と,
Bの標本(データの個数nB=30,平均値XB-=92.5,標準偏差sB=11.643)を一つにした平均値と標準偏差を求めてみましょう.
計算は次の通りです.
データの個数(n)は,
n=∑ni=nA+nB=20+30=50
合計値(T)は,
TA=XA-×nA=89.75×20=1795 ,TB=XB-×nB=92.5×30=2775
合計T=∑Ti=4570
平均値は,
X-=T/n=4570/50 =91.4
偏差平方和は,
S=∑Si+∑ni(Xi--X-)
【SA=sA2(nA-1)=41.77×19=793.63】
【SB=sB2(nB-1)=135.559×29=3931.21】
から、
SA'=793.63+20×(89.75-91.4)^2=848.08
SB'=3931.21+30×(92.5-91.4)^2=3967.51
合計 S=SA'+SB'=848.08+3967.51=4815.59
よって,
分散は,
V=S/(n-1)=4815.59/49=98.277
標準偏差は,
s=SQRT(V)=4815.59/49=9.913
となります.
戻る 次へ 目次へ TOPへ