- 標本での標準偏差(s)はデータ個々のバラツキを,標準誤差(SE)は標本平均(X-)のバラツキを表すものです.1つの標本平均から母集団の性質を記述するのであれば,標準偏差ではなく標準誤差を用います.
- 標準偏差を計算する段階で我々は偏差平方和(S)をn-1 で割り,分散(V)をV=S/(n-1)から求めました(2章). もしここでV=S/nとしていると,分散の期待値 E[V]=(n-1)σ^2/n<σ^2となり,nが小さければ真の母分散(σ)よりも過小になります.
- 普通,n個のデータは平均値(X-)と標準偏差(s)に要約されます.これに対し,母集団での母平均(μ),母分散(σ^2),母標準偏差(σ)を母数(θ)と云います.
そして,標本からの統計量が母数(θ)に一致する場合には,その統計量を不偏統計量と云い,とくに母数(θ)を推定るものであれ,それを不偏推定量と云っています.
3章 比較の考え方を知る.
医学では測定によって得られたデータの性質を統計的に記述したり,加工をほどこして,何らかの研究目的に合った客観的な判断材料を提供しようとします.とくに,医学と医学に関連した研究の多くは比較における判断であり,我々は比較のためにデータをとっていると云っても過言ではないでしょう.
最近のパソコンによる統計ソフトの普及によって,我々はデータの吟味をおろそかにしていないでしょうか.ここでは,医学での統計で最も大切な検定と推定の問題を具体的に説明しましょう.
それは母集団に関する仮設の検証と推測の問題になります.
3.1. 検定の問題について.
正規母集団からとられたn個の標本の各平均値をX1-,X2-,・・・,Xn-とするとき,その個数nを大きくして行くとその平均値(X=)は母平均(μ)に,その標準偏差はσ/SQRT(n)に近づきます.
これは離散量の分布でも同様です.これを中心極限定理と云い図18のように示すことが出来ます.このことを例を挙げて説明しよう.
図18 中心極限定理を表す平均値(X=)の分布
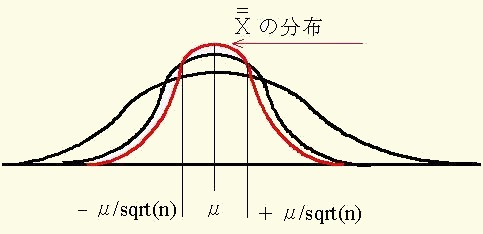
正規母集団から繰り返しとられた
データの平均値はX=の分布に近づく。
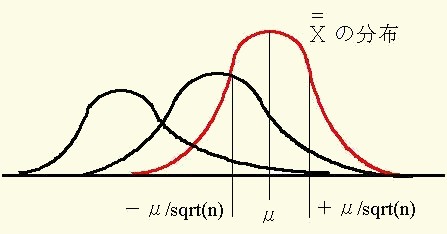
2項分布やポアソン分布においても
繰り返しとれれたデータの平均値は
X=の分布に近づく。
3.1.1. 正規分布にかかわるとき.
40才~49才の成人男性1000名の収縮期血圧を調べたとき,その分布が図19に示すようなヒストグラムであったとします.
図19 母集団を想定した収縮期血圧
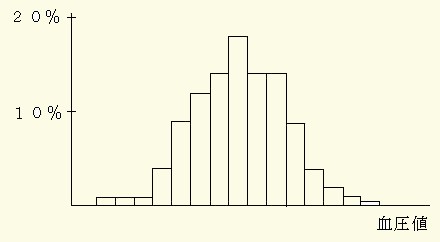
仮にこれを平均値がμ=131 mmHg , 標準偏差がσ=19.2mmHgである母集団とします.そして,
この母集団から繰り返しとった20個の標本(各標本のデータの個数は20)の各平均値 (X1-~X20- )が次の通りであったとします.
( 1)133.8,( 2)134.4, (3)125.5, (4)134.8,( 5)126.0( 6)131.1, (7)129.4,( 8)135.6 ( 9)133.6,(10)138.0
(11)132.4,(12)135.9,(13)126.6,(14)123.9,(15)134.8(16)128.8,(17)137.0,(18)129.8,(19)140.5,(20)128.9
この20個の標本の平均値(X-)はX-=132.04mmHg,標準偏差(sx)はsx=4.55mmHgです.
ここでの平均値(X-)は1000 名の平均値(母平均値 )μ=131 mmHgに極めて近いことがわかります.また,
その標準偏差はsx=4.55mmHgであり,この値は1000 名の標準偏差(母標準偏差 )のσ/SQRT(n),すなわち19.2/SQRT(n)=4.29 mmHg に極めて近いことが分かります.
図20をみて理解して下さい.
図20 収縮期血圧を母集団と想定したときの標本平均(X=)の分布 注釈表示
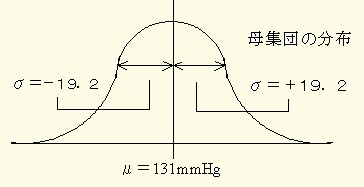
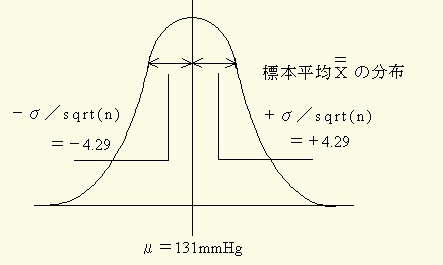
同一母集団からとられた標本平均(X=)は、
この様な分布に近づく.
このようにに平均をμ,標準偏差をσとする正規母集団から無作意にとられたn個の標本の平均値は,母平均をμ,母標準偏差をσ/SQTRT(n)とする母集団に近づくことになるのです.
これは統計的検定や推定を行う上で大切な知識として憶えておいて下さい.そして,
これは正規分布と正規分布から導かれる統計量の分布,すなわちt分布,F分布,χ^2分布などの基本となります.
統計をとる目的の1つは,母集団について推察することでした.すなわち,
① 収集したデータが母集団からのデータであると仮定して検定を行うこと.
② 収集したデータの母集団における統計量を推定すること.
これが統計的現象の把握と,統計的特性の分析に求められる手法と云えます.
我々が医学研究の過程において実際に手にするデータは,その時点においてただ1つの標本です.
たとえ同じ実験を繰り返し行ったとしても,その時点あるいは最終的には,ただ1つの平均値でしかないのです.したがって,
n個の標本の平均値(X=)は,ただ1つの平均値(X-)を期待する値であるので,これをE[X-]と書き期待値(Expectation )を表します.
同様に,平均値(X-)の標準偏差(sx-)も,ただ1つの平均値に対する標準誤差であり,これをD[X-]と書き期待値(Dispersion )を表します.
両者はE[X-]=μ ,D[X-]=σ/SQRT(n)の関係が成立します.
注釈表示
ここで,再び母集団を仮定した 1000 名の血圧値のデータを用いて,20個の標本の平均値が確かに母集団に近づくことになるか,どうかを検定してみましょう.まず,1つの標本の平均(X-)と母平均(μ)の偏差(X--μ)を標準偏差を単位とする値に変換します.
すなわち,標本(1)の平均値(X1-)を対象にするならば,
Z0=(X1--μ)/(σ/SQRT(n))=(133.8-131)/(19.2/sqrt(20))=0.65
から,Z0値は極めて0値に近いことが分かります.これは母集団の平均値とあまり差の無いことを示しています.したがって,
この標本は母集団(1000名の血圧値)のデータからとったものと云えるでしょう.その他の標本の各平均値についても同様のことが云えます.
この様に,「検定の問題」は母集団に関しての知識ないし予想の真偽を問うのに対し,「推定の問題」は標本の統計量から母集団に関する知識を得ようとするものです.
なお「推定の問題」は「3.3.」で説明します.実際の検定では,次の手順にしたがって,検定の問題を考えます.
①検定の問題を明らかにする.
例えば「20 人の血圧の平均は1000名の平均と差はないか?」と問う.
②仮説の設定を行う.
帰無仮説(H0):X-=μ;標本と母集団の平均は等しい.
対立仮説(H1):X-≠μ;標本と母集団の平均は等しくない.
帰無仮説(H0)は,この仮説が真であるか偽であるかを問うものであり,これが「無」に帰することを予想するところからつけられた名称と云われています.ここでは,先の標本(1)の平均値(X1-)について検定してみましょう.
すなわち,
「20人の血圧の平均は1000名の平均と差がない」
ことを疑問として検定を行います.
対立仮説(H1)は,帰無仮説が受け入れられなかったときに採用する仮説であり,ここでは,
「20人の血圧値の平均は1000名の平均と異なる」
とします.
③危険率を設定する.
有意水準(α)=0.01,危険率(α×100)=1%
有意水準(α)=0.05,危険率(α×100)=5%
帰無仮説(H0)を採用するか,しないかの判断は予めその境目となる水準をきめておきます.
この水準になるものが(α)であり,これを有意水準と云います.そして,α×100 %を危険率と云います.
通常,危険率は1%と5%がよく用いられますが,あくまでも検定の問題によって決めるようにして下さい.
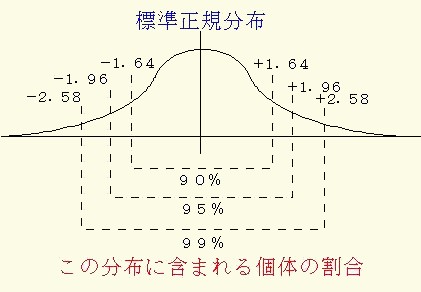
このことは,下の図21のN(0,1)の分布において,ある標本の平均(X-)がX-±2.58×σ/SQR(n)または,X-±1.96×σ/SQRT(n)の範囲内にあれば,その範囲内のデータの割合は,分布の全面積の 99%と95%に相当します.
したがって,その範囲外に出る危険率は1%,と5%となります.仮説の採択は,次の検定統計量(Z0)により行います.
④検定統計量(H0)を計算する.
検定の問題によって,計算が異なりますので4章以降を参考にして下さい.
ここでは,標本(1)の血圧の平均値(X1-)の分布が母平均(μ),標準偏差(σ/SQRT(n))の正規分布に近づくことを利用して,X1-を平均が0,標準偏差が1になるように標準化するとZ0=0.65(検定統計量)となります.
図21はこの様な検定の手順を模式図の分布で示したものです.
図21 検定における分布の考え方
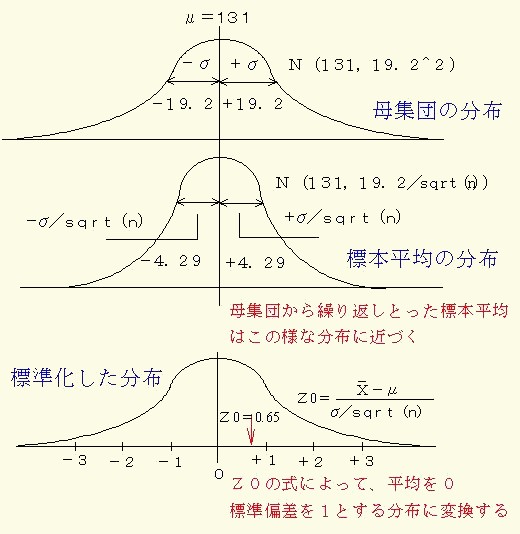
⑤統計的判定をおこなう.
図21において検定統計量 Z0=0.65 は,標準化した分布N(0,1)からの偏差値となります.
これを正規分布表(表計算ソフト「エクセル」から求める)のZ(α)の値と対応づけ,統計的判定をおこないます.
判定は帰無仮説(H0)に対して,
Z0≧Z(α)ならば,危険率100×α%でH0を棄却する.
Z0<Z(α)ならば,危険率100×α%でH0を採用する.
ここでは,
Z0=0.65<Z(0.01/2)=2.576 であるので,危険率1%で帰無仮説(H0)を棄却できません.すなわち,
「20名の平均値は1000名の平均値と差がないと云える」
表計算ソフト「エクセル」からの求め方.
関数式による方法
=NORMSINV(0.005)
関数式の結果は-2.5758を得る.ここでの有意水準(α)はα=0.01/2=0.005を代入する.
これは正規分布での両側確率(α/2)です。
これについては「3.2. 両側検定と片側検定について」で説明する.
ここで注意すべきことは,有意水準(α=0.01,危険率1%)を検定統計量(Z0)をみてから,決めてはいけません.
よく「p<0.01」の表現を見かけますが,これは結果を知ってから有意な差の度合を示す指標として用いるものなのです.しかし,医学や医療の現場では探索的統計分析の手法をとることが多く,「p<0.01」の様なp値による表現を多用しているようです.
今までの説明は,正規分布に従う標本での検定でした.この様に正規分布の仮定のもとでの検定を「パラメトリック検定」と云います.この検定では母集団に対する知識と,母集団が正規分布であると云う仮定が求められます.
しかし,現実には母集団に対する知識や正規分布の仮定が極めて困難なときも,また標本が定性的あるいは質的データのときもあります.この様なとき,検出力の少々の低下があっても,母集団での分布にかかわらず検定する方法が「ノンパラメトリック検定」です.
いずれにおいても検定統計量がある特定の値であるか,どうかを統計量分布から判断し,検定を行なうことに変わりありません.
戻る 次へ 目次へ TOPへ