- 帰無仮説(H0)が正しくないとき,H0を棄却する確率は「1-β」である.これを検出力と言う.
普通,有意水準( α )の約4倍程度が目安となる.α=0.01ならば検出力は約96%~96%程度である.
3.1.2. 離散量にかかわるとき.
通常,離散量のときは比率(百分率)が検定での問題となります.例えば,A・Bの2つの標本において,2つの観測すべき特性ごとにデータを分類し,表8のような度数表が作られたとします.
| - | 有効(Ⅰ) | 無効(Ⅱ) |
| 実薬(A) | A=15例 | A= 5例 |
| 偽薬(B) | B= 5例 | B=18例 |
これを2×2分割表あるいは4分表と云い,医学の分野で良く用いれる比率検定での一般的な形式です.
ここでは,実薬と偽薬の有効・無効の効果率を比較したとき,この度数がとられた母集団において,その効果率に差があるか,どうかを検定するものです.
この様な検定を χ2検定(Chi-Squared test)と云います.
そして,先の正規分布にしたがう検定 (3.1.1.) と同様に,帰無仮説(H0:PA=PB)を採択するかどうかの判定を行うための検定統計量(χ02)を以下の手順で求めます.
ここでは表計算ソフト「エクセル」での方法を順次示します.
●エクセルによる手順(Sheet/sample1)を見て下さい。
ここで,検定統計量(χ02)は各セルにおける「(実測度数-期待度数)2/期待度数」の合計であり, 表8での検定統計量は χ02=12.198となります.
この検定統計量によって決定結果が決まります.
そして,この検定統計量の値が小さいほど2標本(A・B間の効果)の差は小さいと言えるのです.
統計的判定は帰無仮説(H0)のもとで,
χ02≧χ2(1,α)ならば,危険率100α%で帰無仮説を棄却する.
すなわち,「有意な差がある」と判断されます.
χ02<χ2(1,α)ならば,危険率100α%で帰無仮説を採用する.
すなわち,「有意な差がない」と判断されます.
なお,χ2(1,α)は表計算ソフト「エクセル」で次のようにして求めると良いでしょう.
「=CHIINV(0.01,1)」(数式の結果=6.634891)
ここでは,χ02=12.198>χ2(1,0.01)=6.635 ですので,
「危険率1%で実薬と偽薬の効果率に差があると言える」と判断されます.
このような2×2分割表では,もっと簡単に表計算ソフト「エクセル」で求めることができます.
●「エクセルによる手順」(Sheet/sample2)を見て下さい。
ここで,検定統計量(χ02,補正なし)=12.198 ,検定統計量(χ02,補正あり)=10.151 となります.
なお,実測度数がある程度以上に大きいときに限り,ここでの検定統計量(補正なし)を用いても差し支えないと言う条件が付いています.
したがって,実測度数がある程度以下に小さければ検定統計量(補正あり)の値を用いる必要があります.
関数式(D6/2)の項を「イエーツの修正項」と言い,修正によって有意になり難くなるので, 常に「補正あり」を用いるべきとの意見もありますが,それは検定の問題によって判断されるべきでしょう.
一応,5以下の度数があるときに「補正あり」を用いる目安にしておきましょう.
分割表は2行2列の「2×2分割表」以外に,m行2列の「m×2分割表」,m行n列の「m×n分割表」などがあります.
いずれの場合も期待度数より検定統計量(χ02)を求めることができます.
しかし,離散量データを検定の対象としながら,実は統計的には連続量分布(χ2)によって検定を行っているのです.
この様な曖昧さに対し「R.A.フイッシャーの直接確率計算法」は,度数の大きさに関係なく正確な計算ができます.
しかし,この計算は少々面倒ですので,詳しくは第4章で述べることにします.
なお,2×2分割表での測度は出現度数であり,比率(%)ではないので注意してください.
以下に表計算ソフト「エクセル」による計算例を示してみましょう.
いま,仮に2つの治療方法(A法とB法)の治療効果の評価を有効と無効の2つに分けて行ったとします.
A法とB法の治療開始日,疾患の軽重や進行あるいは年齢などに大きな差がなく,A法とB法を比較するうえで,とくに問題はないとします.
そして,一定期間治療を続けたのちの臨床的な治療効果の評価は,
A法:44例のうち有効21例(47.7 %),無効23例(52.3 %)
B法:43例のうち有効28例(65.1 %),無効15例(34.9 %)
であったとします.
これによるとA法よりもB法の方が有効の割合が大きく,無効の割合が小さいので,B法の方が優れているように思われます.
本当にそうでしようか?
統計的にはこの差が有意であるか,どうかを検定しなければなりません.
検定は2×2分割表によるχ2検定を行います.χ2検定は次の通りです.
データを2×2分割表にまとめると表9のようになります.
| - | A法 | B法 |
| 有効 | 21例 | 28例 |
| 無効 | 23例 | 15例 |
● エクセルによる手順(Sheet/sample3)を見て下さい。
この結果から,
χ02=2.013<χ2(1,0.05)=3.841 または,
p=0.156>α=0.05 から,
「危険率5%で有意な差があるとは言えない」と判断されます.
(医学の分野ではp値で表現することが多いようである)
すなわち,A法とB法の臨床的な治療効果の評価に差のないことを示していると判断されるのです. この様に主観的な割合だけでは判断できないことが分かったと思います.
一方,治療効果の割合(比率%)からも検定することができますが, 詳しくは4章でその実際を述べます. この様な手法は医学における統計でしばしば用いられます.
例えば,運動前後における尿中蛋白の測定において,表10の成績を得たとします.
| - | 運動前 | 運動後 |
| 蛋白(-) | 17 | 14 |
| 蛋白(+) | 5 | 17 |
尿中蛋白の出現は運動と関係があるでしょうか?
「エクセル」の計算結果は次のとおりです.
●エクセルによる手順(Sheet/sample4)を見て下さい。
χ02=4.222>χ2(1,0.05)=3.841 または,
p=0.04<α=0.05 から,
「危険率5%で有意な差があると言える」と判断されます.
すなわち,「運動前後の尿蛋白の出現率に差のある」と云えます.
以上の検定では,「有意な差」を検定の問題としました. もし「有意な差」があると判断されたとき,それはいずれか一方との差であるはずです.その差を検定において問う場合もあります.
それが次節(3.2.)述べる両側検定と片側検定です.また,我々は常に検定において2つの誤りをおかす危険があります. それについて次節で説明しておきましょう.
3.1.3. 検定における2つの過誤.
検定において常に注意すべきことは,帰無仮説(H0)が本当であるのに,これを棄却したり,反対に(H0)の採用が誤りであるのに,これを採用したりする危険が伴うことです.
この様な前者の誤りを「第1種の過誤( α 水準での)」,後者の誤りを「第2種の過誤( β 水準での)」と云います.
しかし,現実にはこの様な過誤が起こったとしても,我々にはその過誤が「第1種の過誤」か,「第2種の過誤」かを判断することが出来ません.確かなことは α 水準を減らせば β 水準が大きくなり,反対に α 水準を増やせば β 水準が小さくなることです.
そこで,一般には α=0.01 , 0.05(危険率 1%,5%)がよく用いられます.しかし,これは標本に対する知識から仮説を支持する積極性によって決めるべき性質のものです.
結局,H0を棄却するとき,その誤りは α 水準以内であるように,またH1を棄却するとき,その誤りは β 水準以内であるように期待して判断を行うべきでしょう.
実際には有意水準として α を設定しているのですが,β がどんな値になっているか分からないのですから,H0が採用されたとしても確信を持って結論することは出来ません.反対に,H0が棄却されたときは,かなりの確信が持てることになります.
この様に「検定の問題」は α 水準の条件下における帰無仮説(H0)の棄却,すなわち「有意な差がある」ことを結論ずけたいためのものと云えます.
このことは表11 のように要約できます.
| 帰無仮説(H0) | 棄却する | 棄却しない |
| 正しいのに | 第1種の過誤(1-β) | - |
| 誤っているのに検出力 | - | 第2種の過誤 |
注釈表示
「第1種の過誤」と「第2種の過誤」における α 水準と β 水準は図22 のように示すことができます.
図22 2つの過誤における α と β 水準
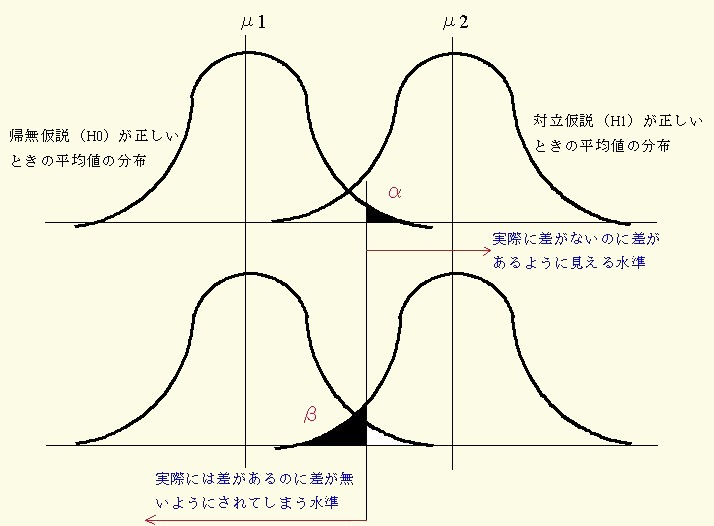
図21 の血圧を例にとると Z0=0.65 が標準正規分布の2.58倍より大きくなる確率、す
なわち、H0が正しいにもかかわらず、H0を棄却する危険率は1/100となります.
これは極めて小さい値ですが、H0の採用には「第1種の過誤」が含まれているので、「
標本の平均値は母集団の平均値と同じである」と結論ずけるのではなく,
「標本の平均と母集団の平均の間には有意な差がない」
と言うべきでしょう.