- 理論的正規分布曲線は次の確率密度関数にしたがってデータが分布している.
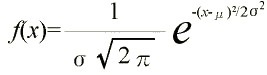
で表される確率密度関数にしたがってデータが分布している. - 医学での問題は硬貨やサイコロの様な確率の計算は少なく,むしろデータとしての離散量(度数や出現率など)である.したがって,その度数や出現率などの分布が2項型か,ポアソン型かを区別しなければならない.
2項分布は医学的アンケートや治療効果の「あり」,「なし」など起こりうる2つの結果を持つ2者択一的な分類尺度(名義尺度)でのデータに適用される.
戻る 次へ 目次へ
2章 基本的な統計量を求める.
前章では,収集したデータを度数分布やヒストグラム,あるいは正規確率紙に整理する方法を学びました.そしてデータの整理はデータの分布を認識することから始まることを知りました.また度数分布などにおいて,そのデータの分布が正規型でないときは,データ変換によってその分布を正規分布に近づける方法も学びました.
2.1. 平均値と標準偏差について.
このように標本としてのデータをもとに,その性質を観察することは,標本が採られた母集団(それは多分に仮説的であるけれども)での性質を観察することなのです.それにはヒストグラムや正規確率紙で視覚的に観察することができますが,もっと具体的に標本としての性質を数字で記述することが求められます.
標本として収集されたデータをもとに,母集団での性質を観察することが,統計をとる目的の1つであると先に述べました.母集団での性質を観察するには,標本についての性質を知らなければなりません.
ここに10人の血圧値を例に説明しましよう.例えば,10人の血圧値を
118,148,128,141,139,120,125,123,134,144
とするとき,そのままでは数字の羅列に過ぎませんが,10人のデータから統計的に少なくとも,次の情報を得ることが出来ます.
10人のデータを代表する値として,
(118+148+…+144)/10=132mmHg
から,その平均値が分かります.次に,データを昇順順位(大きさの順に並べること)にしてみましょう.
118<120<123<125<128<134<139<141<144<148(mmHg)
この血圧値の分布は,118 ~148 mmHg の範囲で一様に分布していることが分かります.そして,その中央値(メディアン)は,128 と 134 の間にあることも分かります.
なお,中央値(メディアン)とは,データを昇順順位としたとき ,ちょうど真中にくる値であり,データ数(n)が奇数の時は (n+1)/2 番目の値が,偶数の時は n/2 番目と n/2 +1 番目の平均値が中央値なります.
すなわち,この例題の場合だとデータ数が偶数であるので,n/2=10/2=5番目 の 128 と n/2+1=10/2+1=6番目 の 134 の平均値 131 が中央値になります(算術平均値132と異なるところに注意して下さい).
平均値は同一母集団からの標本であるとき,比較的変動の少ない値をとるところから,連続量のデータにおいて良く使用されています.
一方,中央値はわずかな異常データに左右されない頑健さはありますが,標本毎の分布によって,その値が変化するので連続量のデータよりも定性的・質的データに良く使用されています.
ここで,血圧値を例に平均値の統計的な性質を考えてみましょう.
図7において,各測定値(Xi)とある値(X0)の差をdi=Xi-X0とするとき,その差diを最小にするようなX0が平均値なのです.図7について云えば
図7 測定値とある特定の値(平均値X0)との差
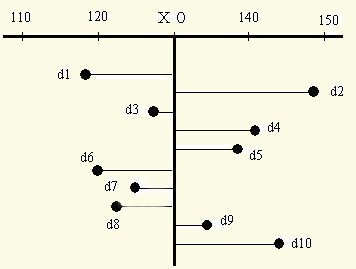
d1+d3+d6+d7+d8)+(d2+d4+d5+d9+d10)=-46+46=0
であるので,この平均値は 132 以外に無いと云うことです.
この様に平均値は,ある特定の値(X0)との偏りを最小にするものなのです.特定の値が平均値である時、この偏りを示すd1+d2+・・・+d10 を平均からの「偏差」と云います.
また,偏差の平方和を「変動」と云い,これをSで表すと,
d1+d2+・・・+d10 =1020 mmHg
となります.そして,
V=S/(n-1)=1020/9=113.333 mmHg
を「分散」と云います.また,
分散の平方根を標準偏差(s)と云い,
s=SQRT(V)=10.646 mmHg
で表わします.これらのことを数式で記述すると次のようになります.
n個のデータをXi(i=1,2,.....,n)とするとき,
その和は,
Tx=X1+X2+‥‥+Xn =∑Xi
その平均(X-)は,
X-=Tx/n=∑Xi/n
その変動は,
Sx=∑(Xi-X-)2=∑Xi^2-Tx^2/n
その分散は,
Vx=Sx/(n-1)
その標準偏差は,
s=SQRT(Vx)
で示されます.これらは,以後の統計的方法を行ううえで大切ですので良く覚えておいて下さい.
ここでもう一度,「例題」の血圧値に注意してみましょう.10人の血圧値は,図8でも分かるように,平均値の左右にばらついています.
図8 10人の血圧値の分布

このバラツキの程度を表す尺度として,一般に標準偏差(s)が用いられます.この血圧値の例では,平均値X-=132 mmHg を中心に±10.646 のバラツキがみられます.
2.2. 正規分布について.
これは,平均値X-±1標準偏差(X-±1s)が121.354~142.646 mmHgであること,そしてデータの68.26%(この例では 6.826 人)がこの範囲にあることを示しています.
このように,標準偏差の値が大きいほど分布の平均値のまわりのバラツキが大きくなることが分かります.
平均値と標準偏差は,以後の統計的検定や推定あるいは,多変量解析などにおいて基本となる大切な計算なのです.
平均値と標準偏差(X-±s)によって,標本に関する性質(バラツキ)を数値で記述することができました.
しかし,標本についての全体的な分布は,度数分布と度数分布にもとずくヒストグラムや,正規確率紙による図形表示の方が認識しやすいと思います.例えば,40名の血圧値が次ののようであったとします.
156,124,116,138,108,133,119,109,152,138
145,156,154,144,113,156,151,134,123,119
118,148,128,141,139,120,125,123,134,144
138,134,126,138,116,130,154,161,132,126
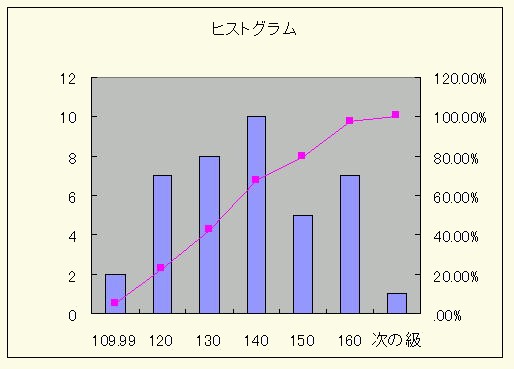
このデータによる度数分布は表4であり,そのヒストグラムは図9のような正規分布に近似します.
表計算ソフト「エクセル」による結果を示します.
| データ区間 | 頻度 | 累積% |
| -110 | 2 | 5.00 |
| 110-120 | 7 | 20.00 |
| 120-130 | 8 | 40.00 |
| 130-140 | 10 | 67.50 |
| 140-150 | 5 | 80.00 |
| 150-160 | 7 | 97.50 |
| 160- | 1 | 100.00 |
図9 血圧値のヒストグラム
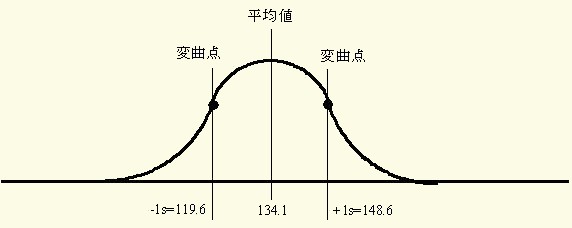
正規分布を模式的に示すと図10のようになります.
正規分布曲線は平均値を頂点に,左右に滑らかな下降曲線の分布を描きます.左右への滑らかな下降曲線は,最初,下に凸の曲線から矢印を境に上に凸の曲線になります.
この矢印の点を変曲点と云い,だいたい1標準偏差(1s)に相当します(図10).先の血圧値の例では,平均値X-=134.075 mmHg , 標準偏差 s=14.455 mmHg であり,119.62~148.53 mmHg の範囲が縦線で囲まれた部分に相当します.
そして,全データの 68.26 %(27.3 人)がこの部分に含まれます.
図10 正規分布の模式図
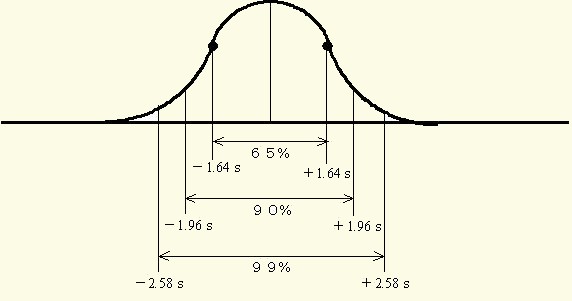
正規分布のもとでの割合は図11のようになります.
図11-1 正規分布曲線のもとでの割合(その1) 注釈表示
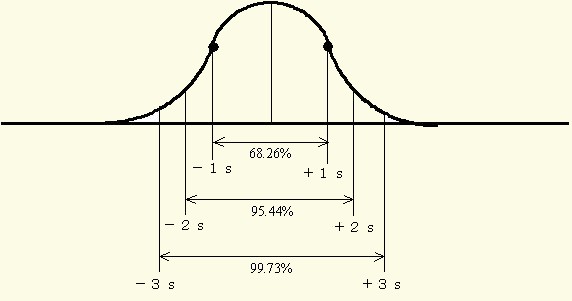
図11-2 正規分布曲線のもとでの割合(その2)
そして,正規分布は平均値と標準偏差によって決まるところから,母集団において N(μ,σ2)で示されます.
なお,μ・σ2・σはそれぞれ母集団での平均・分散・標準偏差であり,標本の分布が正規型であれば標本でのX-・s2・s
はそれぞれμ・σ2・σ の推定値と見なされます.また,正規分布はガウス分布とも呼ばれ,以後の統計的方法で最も重要な役割を果たすことになります.図11の割合を覚えておくと便利でしょう.
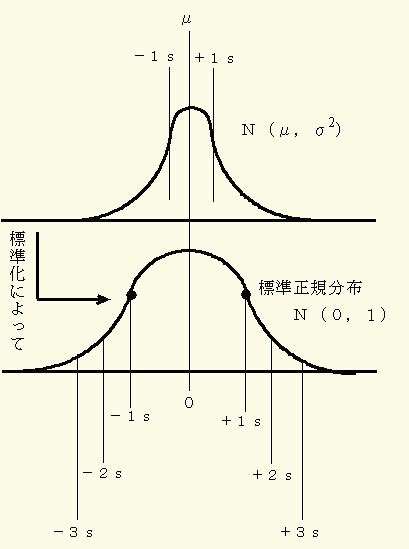
次に,N(μ,σ2)の正規分布において,ある任意の値をX0とするとき,ここのX0に対して,
Z=(X0-μ)/ σ
の変換を行うと,その分布は母平均をμ=0,母分散をσ2=1とする正規分布N(0,12)にしたがいます.これを標準または規準正規分布と云い,図12のように示すことが出来ます.
統計的検定や推定の問題では,N(0,12)の確率分布Pr(Z)において,Zがある値になる上側または下側確率Pr(Z)を求めたり,あるいは,Zがある値以上になる確率Prを与えてPr(Z)のZ値を求めたりします.
なお,上側または下側確率とは,正規分布が左右対称であるので,上側確率は+Z,下側確率は-Zとなります.詳しくは次章で説明しましょう.
正規分布または正規分布近似であれば,平均値と標準偏差によって,データに関する種々の情報が得られることが分かりました.次章の検定や推定の問題では,この正規分布の仮定のもとに,統計的な種々の検定や推定が行われるなど大切な分布と云えます.
図12 正規分布の標準化
しかし,母集団からの標本が常に正規分布またはそれに近い分布とはかぎりません.例えばデータが,
①2項分布に近似しているときは,sin-1 QRST(x/n)によって変換を試みると良いでしょう(変換には逆正弦変換表などを用いると便利です).
②ポアソン分布に近似しているときはSQRT(x),SQRT(x+1/2),log(x)によって,正規型への変換を試みると良いでしょう.
特に,ここではデータ変換で誤りやすい「sin-1 QRST(x/n)」について説明しましょう.これは,逆正弦変換(角変換)と云い,出現率など(%)でのデータを角度に変換するもので,医学でよく用いられています.
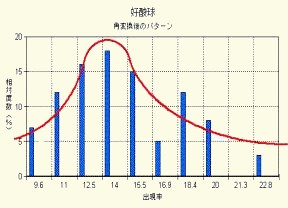
一例を挙げると,非発作時における気管支喘息患者(70名)の末梢血中に出現した好酸球数の全白血球数に対する割合(%)が,図13-1のヒストグラムであったとき,好酸球数の出現率は0%~100%の値しかとらないので,(%)を角度に変換して正規化を図る必要があります.
図13-2は角変換後のヒストグラムであり,ほぼ満足すべき結果を得ていることが分かります.
図13-1 好酸球数(%)の角変換前の分布
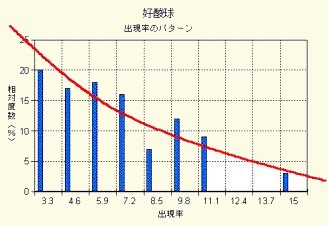
図13-2 好酸球数(%)の角変換後の分布
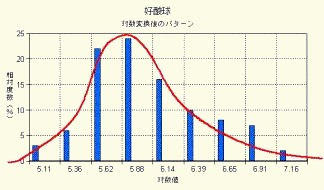
では, 1mm3中の好酸球数を計ったときはどうでしょうか.それは当然,連続量として処理すべきであり,そのヒストグラムは図14-1で示されます.1mm3 中の好酸球は log 変換によって,図14-2のように正規型を得ることができます.
図14-1 好酸球数(mm3)の分布
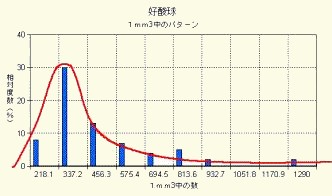
図14-2 log変換後の分布
このように2項分布する出現率などを,連続量としてデータ変換するのは誤りです.しかし,変換式の選択は絶対的なものではなく,ある程度の試行錯誤を必要とします.また無闇に変換すると,データ本来の性質を失う危険もあるので注意して下さい.
戻る 次へ 目次へ TOPへ