9.8. 傾向スコアー法(Prepensity Score:PS )
2値の目的変数に対して複数の説明変数で予測や説明変数の有意性を判断するとき,説明変数間の影響を除いたり調整したりして2群間の差を見る方法です.
その手法のうちで最も一般的な傾向スコアによる”full matching”について紹介します.
例題データは「R package」から引用し,分かり易い様に多少の編集を加えました.
# R program の例.
library(Matching)
data(lalonde) # データとして”lalonde”を用いる
dat<- lalonde[, c(3:6,10,11,12)] # lalonde の中の2値データを抽出する.
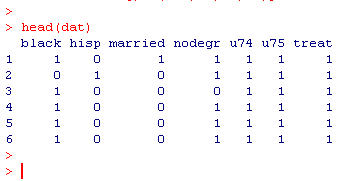
head(dat) # データ lalonde の確認(図1)
図1: lalonde から抽出した2値データ(名義尺度)
■ 変数の意味.
treat=treatment status (職業訓練受講の有無)
black=black person
hisp=hispanic
married=married person
nodegr=high shool diploma
u74=earnings in '74
u75=earnings in '75
attach(dat)
fit<- glm(treat~ ., data=dat, family=binomial) # logistic regression analysis
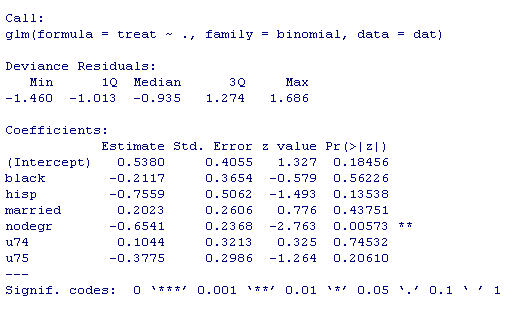
summary(fit) # Logistic analysis の結果(図2)
図2:Logistic analysis の出力結果
PSpos<- round(fit$fitted.values,3)
PSneg<- round(1-fit$fitted.values,3)
PS<- vector(length=nrow(dat))
PS[dat$treat==1]<- PSpos[dat$treat==1]
PS[dat$treat==0]<- PSneg[dat$treat==0]
Weight<- round(1/PS,3)
dat<- data.frame(dat, PSpos, PSneg, PS, Weight)
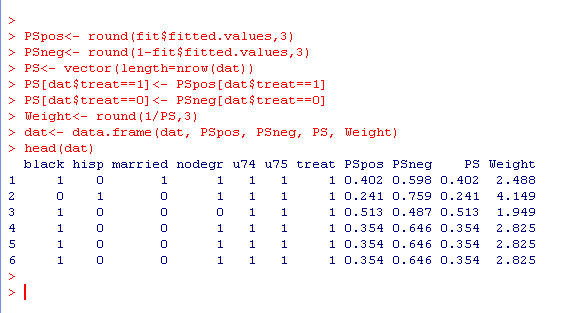
head(dat) # propensity score (図3)
図3:propensity score のデータテーブル
PS.mat <- Match(Y=NULL, Tr=dat$treat, X=fit$fitte, replace = F, caliper=0.1)
summary(PS.mat)
# オプション
# PS.mat<- Match(Y =NULL, Tr =dat$treat, X =fit$fitted, estimand ="ATT", M =1, ties =TRUE, replace = TRUE)
# PS.mat<- Match(Y =NULL, Tr =dat$treat, X =fit$fitted, estimand ="ATC", M =1, ties =TRUE, replace = TRUE)
# ATC=対照群,ATT=処理群,caliper=取り敢えず0.1で試す
summary(PS.mat) # PS matching 統計量(図4)
図4:PS matching の統計量(因果効果の推測)

N<- length(PSmat$index.control)
PS_match<- dat[c(PSmat$index.control, PSmat$index.treated),]
PS_match<- data.frame(PS_match, Matched_ID=rep(1:N, 2))
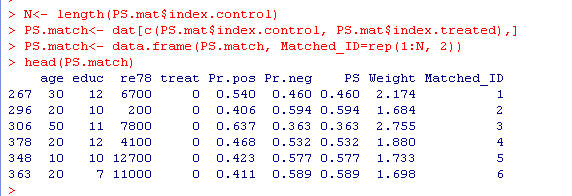
head(PS_match) # PS matching 後のデータテーブル(図5)
図5:PS matching の確認
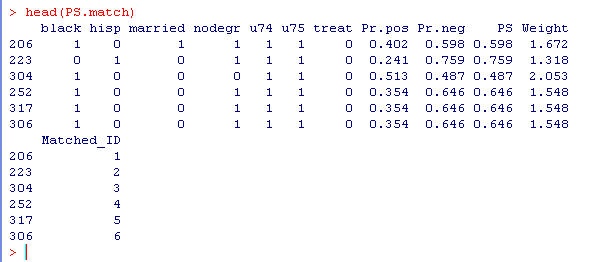
図5のmatching データ(PS_match)を用いて matching 後の検定などを次の様にして行います。
matching 後のデータをファイルに書き出し、必要に応じて読み込んで使用すると便利でしょう。
write.csv(PS.match, "PS_match.csv") # matching データの書出し
PS_match<- read.csv("PS_match.csv") # matching データの読み込み
# matching 前のカイ二乗検定
table(dat$black, dat$treat, deparse.level=2)
chisq.test(table(dat$black, dat$treat))
table(dat$hisp, dat$treat, deparse.level=2)
chisq.test(table(dat$hisp, dat$treat))
# matching 後のカイ二乗検定
table(PS_match$black, PS_match$treat, deparse.level=2)
chisq.test(table(PS_match$black, PS_match$treat))
table(PS_match$hisp, PS_match$treat, deparse.level=2)
chisq.test(table(PS_match$hisp, PS_match$treat))
以上の結果をまとめると,図6の結果となります.
図6:matching 前と後のカイ二乗検定結果
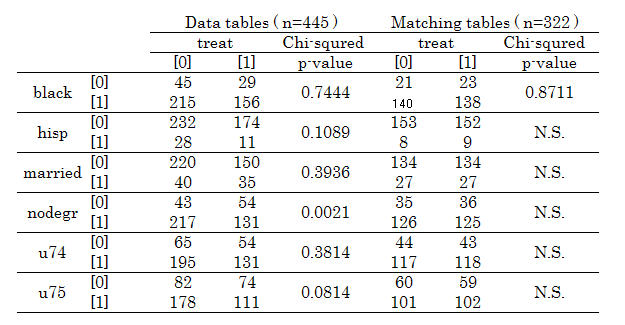
maching 前後の p値を見ると説明変数(nodegr)が有意でなくなっており,変数間での調整(効果)が分かります.
以上は,2値データ(名義尺度)の場合でした.
■ 連続量の場合は次の様にして実行して見ましょう.
dat<- lalonde[, c(1,2,9,12)]
データを分かり易いように、次の様にして少し改変してみます。
dat$age<- floor(dat$age/10)*10
dat$re78<- floor(dat$re78/100)*100
dat<- subset(dat, dat$re78>0)
head(dat, 20) # 連続量の抽出(図7)
図7:例題としての連続量
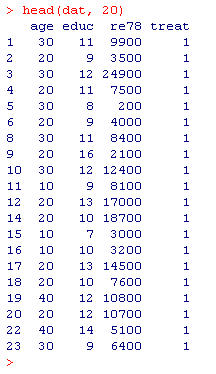
■ 変数の意味.
re78=real earnings '78
2値データの場合と同じように実行すれば良いでしょう.
"lalonde"のデータは正規分布と言えないので、検定は「Wilcoxon test」(Asymptotic Wilcoxon rank sum test)を用いることにしました.
正規分布で等分散が仮定できるなら「two sample t-tast」(matching 後は 「paired t-test」)を用いる良いでしょう.
図8:連続量における Logistic analysis の出力結果
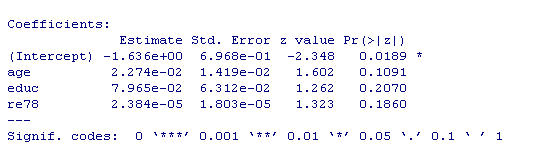
図9:連続量における propensity score のデータテーブル
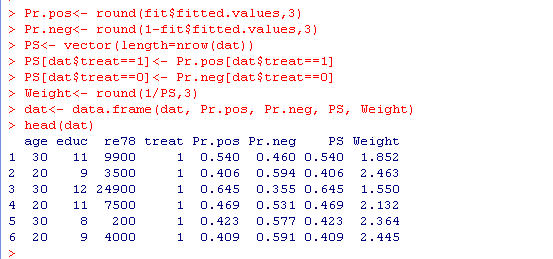
図10:PS matching の確認
matching 前後での分析結果(統計量)は図11 の通りです.
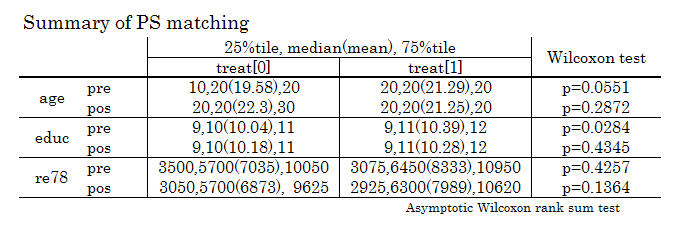
(pre=matching 前,pos=matching 後)
PS matching では,やたらに説明変数を増やせば matching 数が極端に少なくなる事もありますので,交互作用や交絡因子の影響を良く考え変数を吟味し実行して下さい.
ここでは、R package のデータ(lalonde)を例題にしましたが医学データでも同じです.
戻る 次へ 目次へ TOPへ