7.3. データを分類する(クラスター分析)
ここではクラスター分析の要点のみを説明します.実際の計算方法などは成書を参考にして下さい.
クラスター分析は判別分析のように予め判別すべきグループに分類できない,または,分類されていないときとか,あるいは,変量間の意味づけが困難なデータに対して有効です.
例えば,表52のデータを判別分析では予め表51のように「低温群」と「高温群」に分類したデータを与えていました.しかし,クラスター分析では個々のデータの所属群を不明として分析を行います.
したがって,多変量解析の順序としては判別分析よりもクラスター分析を先に行うべきかもしれません.
下記の表52(一部のデータ)をもとにクラスター分析の一例を示してみましょう。
スギ花粉データと気象条件から抜き出したデータ
| 花粉数 | 気温 | 湿度 | 天気 |
| 4.3 | 4.1 | 77 | 3 |
| 2.2 | 5.1 | 74 | 3 |
| 4.6 | 6.2 | 76 | 3 |
| 11.1 | 6.8 | 58 | 2 |
| 29.9 | 14.2 | 58 | 2 |
| 36.5 | 14.9 | 56 | 2 |
クラスター分析を行う前に表52のデータの性質について少し考えてみましょう.
それには各観測時点の花粉数・気温・湿度・天気にともなう標本の変化を図52 のようなグラフにしてみると良く分かります.
図52 スギ花粉数と気象条件に伴う標本の変化のパターン
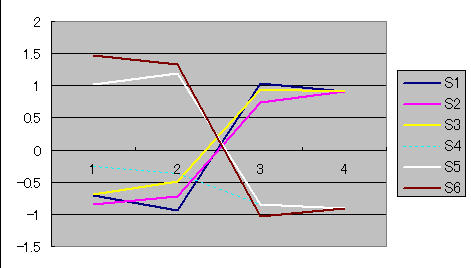
このグラフを見ると標本S1,S2,S3と標本S5,S6の変化がパターンとして類似しており,標本S4が他と異なっていることに気づきます.
なお,図52ではデータの変量間の単位を同一にするために標準化変量を与えています.
この知識をもとにクラスター分析を行ってみましょう.
はじめにクラスター分析の最短距離法と言う手法を用いてデータを予備的に分類してみます.
図53は最短距離法(標準化ユクリッド距離)によるデンドログラム(樹状図)です.
図53 最短距離法によるデンドログラム
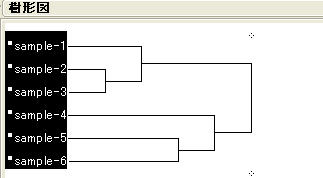
この図から,標本S1,S2,S3と標本S4,S5,S6の2群に分類できることが分かります.
次にウォード法と言う手法を用いますと図54 のようになります.
図54 ウォード法によるデンドログラム
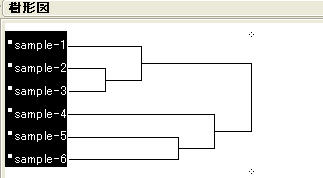
図53と図54でのクラスター形成過程は同じです.
このようにクラスター分析などの多変量解析では分析する者の専門的な知識をもって結果の判断とさらなる分析の配慮が求められます.
7.4. 多変量要約のための解析(主成分分析)
m 個の変量からなるn個のデーターは m 次元空間に分布し,それぞれ相互に関連する何等かの主要な成分を包括していると考えられます.
主成分分析は多次元空間に分布するデーターの主要な成分を2次元座標に縮約してデーターの持つ主要な変動を把握するものなのです.例えば,
A病棟とB病棟の入院患者について嗜好物の調査をし好みの順位をつけたところ表52 の結果になったとします.
表52 入院患者の嗜好物の順位
| 病棟別 | 肉類 | 魚介類 | 野菜類 | 豆・種実類 |
| A病棟 | 1(とても好き) | 2(好き) | 4(きらい) | 3(普通) |
| B病棟 | 2(好き) | 1(とても好き) | 3(普通) | 4(きらい) |
これを2次元座標にプロットすると図55の様になります.
図55 病棟別入院患者の嗜好物の主成分散布図
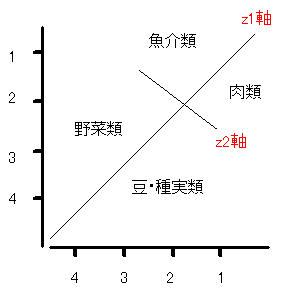
すなわち,Z1 はA病棟とB病棟に共通した嗜好物の順位を示しており,その順位は肉類, 魚介類,豆・種実類,野菜類の順序であることが分かります.
このZ1 ベクトルを第1主成分と云い,第1主成分の共通の因子はコレステロールの高い順序かも知れません.
次に,第1主成分と直交するようなベクトル(Z2)を第2主成分と云い,これはZ1 軸上に現れなかった因子を示しています.そして,
第2主成分の共通因子は「肉料理を中心にした洋食」と「魚料理を中心にした日本食」を示しているようです.
もし,Z2軸をより詳しく検討すればA病棟とB病棟での「年齢構成」とか「疾患との関連」などを発見するかも知れません.
この様に,主成分の因子はあくまでも専門的な知識や経験によって決まるものなのです.同時に,n個のデーターから等質なものと異質なものを発見し新たな要因の探求に効果を発揮する場合もあります.
図56は某年3月〜4月の岡山市内における前日・当日のスギ花粉飛散数と気象条件をもとに,主成分分析を行い標準化したデータの主成分スコアーを2次元座標にプロットしたものです.
図56 スギ花粉飛散と気象条件の主成分散布図
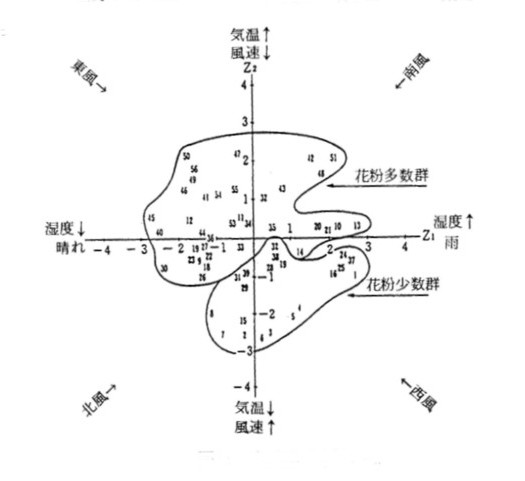
第1主成分(Z1),第2主成分(Z2)をそれぞれ Z1, Z2 とするとき,Z1 軸は湿度を,Z2 軸は気温と風速を表していると考えられます. そして,
2次元座表上の各スコアーは,「花粉小数群」と「花粉多数群」に分離できる傾向が認められます.
この様に主成分分析は観測の対象であるデータに潜在する等質あるいは異質の群を見いだしたり,主成分軸の意味づけと多変量の記述を簡約するのにとても有用です.
応用例として症状・徴候からの総合判断のための解析などに用いられています.
戻る 次へ 目次へ TOPへ