戻る　　　　　次へ　　　　　目次へ

6.3.　相関と回帰について．
２次元正規分布の母集団からとられた標本は直線回帰によって，その相関性を記述することができます．相関係数とそれに関する検定や推定の問題は,
2つの標本間の関連性の測度と，その信頼性を保証するものです．例えば,
例題30 のデータ（成人50名の血圧値）を連続量として表計算ソフト「エクセル」で求めて見ましょう「エクセル→分析→ツール→回帰分析」。
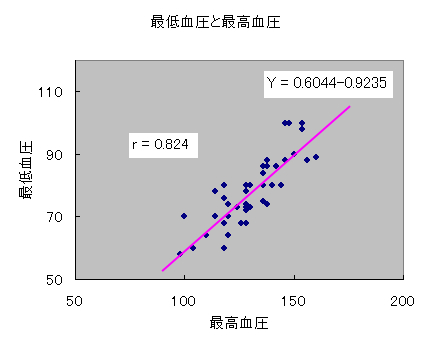
分析結果は図41 の通りであり,最高・最低血圧の間にはｒ＝0.824 で相関性のあることが分かると共に，最高血圧(ｘ)と最低血圧(ｙ)の間には,
ｙ＝0.6044ｘ−0.9235 の１次式で示されるような１次線形回帰,すなわち，直線回帰へのあてはめが認められます．
これを最高血圧(ｘ)に対する最低血圧(ｙ)の回帰式と云い，一方の変量(ｘ：独立変量)が与えられた条件のもとで，他方の変量(ｙ：従属変量)の値を予測することが出来るものです．
例えば，最高血圧が 180 mmHg であれば，最低血圧は，
ｙ＝0.6044ｘ−0.9235＝0.6044*180−0.9235＝107.87 mmHg

近い値をとると予想されます．
逆にｙの値を与えて，回帰直線と交わる点に対応するｘの値を求めるときもあります．例えば，医学での実験などでは，標準物質の濃度(ｘ)を変えて，その濃度に対する吸光度(ｙ)を求め検量線とするものがそうです．
検量線では，ある未知の物質の吸光度を検量線にあてはめて，その濃度を求めます．これは回帰直線を利用した逆推定と云えるでしょう．医学や医療の現場では，日常的に，この様な相関と回帰の計算が統計学を意識せずに実行されています．
検量線としての回帰直線は，統計用語で線形校正あるいは線形校正直線と云います．相関と回帰の問題は直線性に限られるものではなく，色々な相関関係が２標本間に存在すると思います．

図41　血圧の相関散布図と回帰直線

6.3.1.　直線関係のとき．
通常,2つの標本の関係はその直線性によって示されます．それは，標本間の関係を最も単純な ｙ＝ａｘ＋ｂ の１次式で説明できるからです．
直線関係の相関と回帰の問題は，先に基礎的な事柄について説明しましたが，ここでは直線回帰の問題を少し考えてみましょう．

［検定の手順］
(1)検定の問題を明かにする．
「２つの標本は相関関係があるか？」

(2)仮説の設定を行う．
帰無仮設（Ｈ₀）：ρ＝0
対立仮設（Ｈ₁）：ρ≠0 （両側検定のとき）

(3)危険率（100α％）を決める．
両側検定の有意水準：α

(4)検定統計量（ｔ₀）を求める．
相関係数(ｒ)の検定において ｎ＝データの個数 とするとき，検定統計量(ｔ₀) は次式により求とめます．
t₀=r*sqrt((n-2)/(1-r^2))

(5)統計的判定を行う．
［両側検定のとき］
ｔ₀＜ｔ(ｎ-2,α)ならば，「危険率100α％で相関がない」
ｔ0≧ｔ(ｎ-2,α)ならば，「危険率100α％で相関がある」

なお，ｔ(ｎ-2,α)は表計算ソフト「エクセル」から求めると良いでしょう．

次に回帰係数，勾配(ａ)の検定は次の検定統計量(t_a)について行います．
t_a=ｒ* sqrt((ｎ−2)/(1-r^2))

これは，相関の検定統計量(ｔ₀)と同じです．

回帰係数と切片(b)の検定は，次の検定統計量(t_b)について行います．
t_b=b/(Ｖ_e*(1/n +Ｘbar²/Ｓxx))　,　 Ｘbar²は平均値の二乗
Ｖ_e=(Ｓyy(1-r²))/(n-2)　，ＳxxとＳyyは偏差平方和

(6)100(1-α)％の信頼限界を求める．
ａ．母相関係数(ρ)の 95％信頼限界は次により求めます． 注釈表示

１．lnは，ある値Ｘについて自然対数LogＸの値を与える．lnＸ＝2.3026×LogＸ で求められる. ２．expは，ある値Ｘについて，指数関数ｅの値を与える．なお,ｅは自然対数の底(ｅ＝2.7183)である． ３．医学での実験などにおいて，相関係数や回帰式は次のような分析誤差の記述などに用いられる.

表計算ソフト「エクセル」の関数を用いると便利です．
関数「= fisher(r)」として,相関係数(r)をＺ変換しＺrを求めます.　次に,
Ｚr±1.96/sqrt(n-3) から下限値(Ｚ_L)と上限値(Ｚ_u)を求めます.そして,
Ｚ値をｒ値に変換しする関数「=fisherinv(Ｚ_L)」,「=fisher(Ｚ_u)」によって95％信頼限界が求まります.
例えば、図41の場合だと、
データ数＝50,相関係数ｒ＝0.824　ですので,母相関係数の95％信頼限界は次のようになります.
t₀=0.824*sqrt((50-2)/(1-0.824^2))=10.076
t₀=10.076>t_0.05=2.012, よって有意であり相関があると言える。

Zr=fisher(0.824)=1.169
ZL=1.169-1.96/sqrt(50-3)=0.883→fisherinv(0.883)=0.708
ZU=1.169+1.96/sqrt(50-3)=1.455→fisherinv(1.455)=0.897

よって、母相関係数(ρ)の95％信頼限界は
0.708＜＝ρ＜＝0.897

となります。 　

ｂ．母回帰係数と勾配(ａ)の100(1−α)％信頼限界は次の通りです．
ａ±ｔ(ｎ-2 , α) * sqrt(Ｖ_e/Ｓxx)

ｃ．母回帰係数と勾配(ｂ)の100(1−α)％信頼限界は次の通りです．
ｂ±ｔ(ｎ-2 , α) * SQRT(Ｖe * (1/ｎ+Ｘbar²/Ｓxx)

「例題31］
次のデータは肺機能検査において測定した努力性肺活量（FVC）と，その１秒量（FEV）です．

番号	1	2	3	4	5	6	7	8	9	10
FVC(L)	4.05	3.67	4.15	2.95	2.35	2.12	3.50	3.32	3.15	2.97
FEV(L)	3.60	2.61	3.11	1.83	1.36	1.70	2.30	2.23	2.62	2.52

このデータを相関図にすると，図42のような散布図となります.

図42　努力性肺活量と１秒量の相関

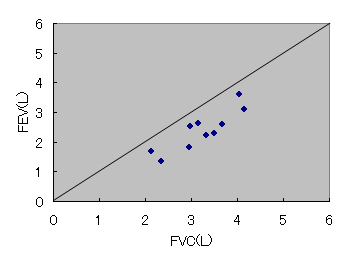
図42 の座標上における散布点は45゜の直線に対してほぼ平行しており，直線関係の相関があると思われます．
回帰式は図43 のように，ｘに対するｙの回帰式は ｙ＝0.883ｘ−0.458 で表わされます．また，
ｙに対するｘの回帰は，ｘ＝0.876ｙ＋1.132　で表わされます．

図43　努力性肺活量と１秒量の回帰式

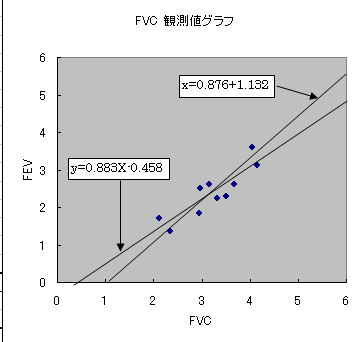
このように，２つの回帰式はともにｘとｙの交点を通りますが，その勾配を異にしています．すなわち，
従属変量をｘにするかｙにするかによって，その回帰式が異なることに注意しなければなりません．
例えば，医学検査では従来法(ｘ)と新法(ｙ)との間の相関と回帰式を求め，回帰式の勾配(ａ)と切片(ｂ)を補正係数とするファクターを定め， 従来法から新法へ，新法から従来法へと測定値を必要に応じて変換することがあります．
この時のファクターの定め方が，従来法に対する新法の回帰であれば，従来法の値を独立変量として計算しなければなりません．

この様に，同じ物質を異な手法あるいは機器によって測定し，両者間の相関と回帰を求めるときは，ｙ＝ａｘ＋ｂ と ｘ＝ａｙ＋ｂ の両方を求めておくと良いでしょう．
ｙ＝ａｘ＋ｂ から， ｘ＝1／ａ（ｙ−ｂ） の 1／ａ　をファクターとするのは，検量線における標準物質濃度と吸光度のように，一方を誤差のないものとして，他方を求めるときに限るべきでしょう．

［例題32］
血清アルブミン値が正常値範囲（4.2〜5.7 g／dl）にある試料10検体を用いて，自動分析機と従来法で同時測定し次のデータを得ました．このデータの相関を求めます．

自動分析	4.5	4.6	4.2	4.4	4.5	4.4	4.0	4.2	4.3	4.3
従来法	4.8	5.6	4.9	5.2	5.0	5.0	5.0	4.9	4.9	5.5

図44 は例題での正常値範囲にある血清検体の相関図であり，その相関係数（ｒ）は，ｒ＝0.343 ，回帰式は ｙ＝0.52ｘ＋2.82 です.

図44　自動分析機と従来法の正常範囲内データの相関

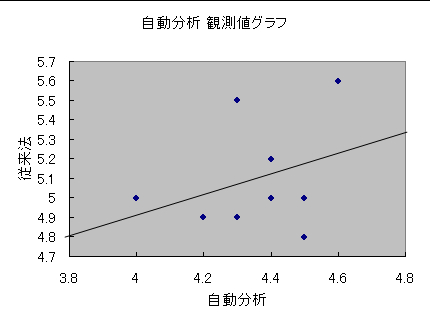
そして，相関係数(r)の検定は，
t0＝1.03＜ｔ（8,0.05）＝2.306 （両側検定，危険率 5％）

から，自動分析機と従来法の間に相関が無いと云えます．
この様な結果について，読者は納得されるでしょうか？

何故なら，同一物質を測定して相関関係がないことに強い疑問を持つに違いありません．新たに次のような低値範囲のデータを追加し相関を求めてみました．

自動分析	2.8	3.7	3.1	2.5	2.2	3.2	2.5	3.9	1.9	2.0
従来法	3.1	4.4	3.4	3.2	2.8	3.6	3.1	4.3	2.2	2.5

図45は低値範囲のデータを加えた相関図です.

図45 自動分析機と従来法の広範囲内データの相関

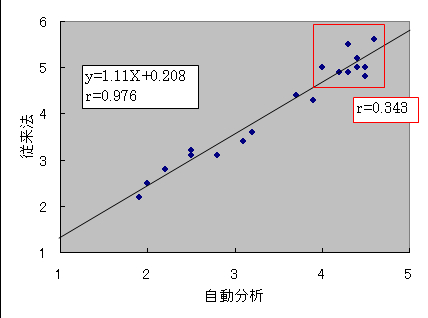
その相関係数(r)はｒ＝0.976 ，回帰式はｙ＝1.11ｘ＋2.08であり，強い相関関係のあることが分かります．
そして，この相関図から，最初の 10個のデータ（正常値範囲）は赤色で囲まれた極く狭い範囲での相関であり，その共変動（積和）は Ｓxy＝0.747 と非常に小さかったことが分かったのです．
この値は血清アルブミン値としては，測定の誤差程度であり，相関係数(r)を求めるには不適当なデータであったのです.

戻る     次へ      目次へ     TOPへ