6.1. 相関表の作り方.
2つの標本(A群とB群)のデータを,2次元度数分布にしたものが相関表です.
相関表は2つの標本の数が多く,1個1個のデータを2次元座標軸上にプロットするのが大変なときとか,あるいは2群のデータの分布や集中の様子などを観察するのに有用です.
[一般形式]
| 分布の度数 | B0〜B1 | Bj-1〜Bj | Bm-1〜Bm |
| An-1-An | * | * | Fnm |
| Ai-1-Ai | Fi1 | Fij | Fim |
| A0-Ai1 | F11 | * | * |
相関表は2標本のうち,一方の群が定性的・半定量的なデータで度数分布で与えられているならば,他方の群が連続量であっても相関表による記述が良いでしょう.
度数分布の作成は,「1.データを整理する.(1.3.度数分布の作り方)」の要領で行います.
相関表の横軸(x)は級限界値の小さい方を左側に,縦軸(y)は級限界値の小さい方を下側にします.そして,縦横軸の級限界範囲内のデータの度数を記入します.
具体的には,次の「例題30」の要領で行うと良いでしょう.
[例題 30] 定期検診で測定した成人 50名の最高・最低血圧を表45 に示します.このデータをもとに相関表を作成してみましょう.相関の問題は「最高血圧の高い者は,最低血圧も高いか」です.
[最高血圧]
148,128,120,118,146,138,114,130,118,136 ,118,124,110,120,140,154,154,100,136,128,128,128,146,156,128
144,120,128,138,126,138,130,118,120,128,136,160,124, 98,104,130,136,114,150,138,118,142,120,128,130
[最低血圧]
100, 68, 70, 68, 88, 86, 70, 73, 76, 86 ,60, 73, 64, 74, 80,100, 98, 70, 84, 78, 80, 68,100, 88, 73
80, 74, 72, 88, 68,88, 80, 80, 70, 74 ,75, 89, 73, 58, 60 ,80, 80, 78, 90, 74,76, 86, 64, 68, 73
相関表の作成は表計算ソフト「エクセル」を使うと便利です。
相関表から求めた相関係数(r)は,
r=0.854
最高血圧(x)に対する最低血圧(y)の回帰式「y=ax+b」で示される回帰係数(a,b)は,
a=0.598
b=-0.437
となります。よって,回帰式は y=0.597X-0.437 で示されます。
6.2. 相関図の作り方.
[一般形式]
散布図の●印は色々な要因ごとに,例えば,年齢・性別・地域などによって,*△◎印などあるいは,色分けするなどして全体の中での要因ごとの相関関係を視覚的に確認できるように工夫することも大切です.
(2)直線関係の負の相関があるとき.
(3)負と正の相関関係が混在するとき.
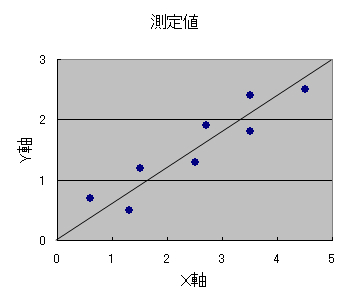
図36 正の相関関係
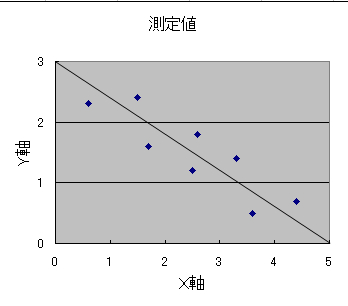
図37 負の相関関係
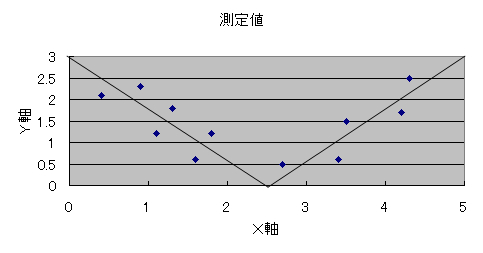
図38 正と負の相関関係
(4)曲線の相関関係があるとき.
図39 のような曲線を当てはめることができます.ここでは一定方向の直線を当てはめることができません.
図39 曲線の相関関係
(5)相関関係がないとき.
以上のように,相関図は2次元座標でのデータのバラツキの様子や全体的な相関関係(直線性)などを視覚的に確認することができます.
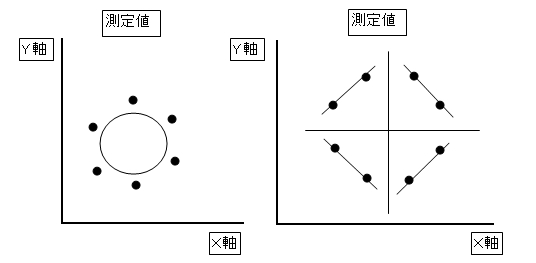
図40 相関関係のないとき
グラフ用紙の横軸(x)に最高血圧などの測定値を,縦軸(y)に最低血圧などの測定値を目盛り,xとyの交点に●印などを付けた「一般形式」のような散布図が相関図です.
相関図は主として連続量のデータに用いられます.
相関図での2標本の関連性は,次のような場合が考えられるでしょう.
(1)直線関係の正の相関があるとき.
図36 のように右上がりの直線となります.
図37 のような右下がりの直線となります.
図38 のようにV字型となります.

この様な場合は,2つの標本の一方の分布が他方の分布と異なっている場合があるので,データ変換(log 変換など)で2次元正規分布とし直線回帰をはかるか,あるいは曲線回帰へのあてはめを考えてみます.
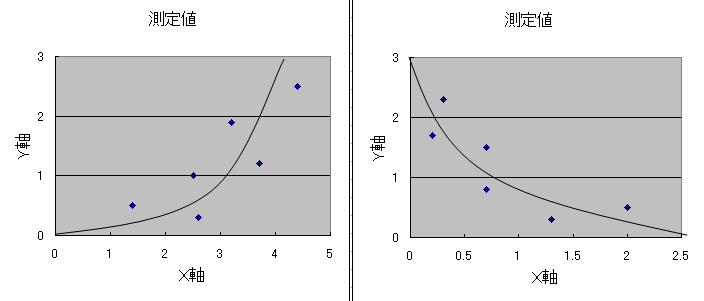
図40 は相関関係のない散布を示しています.相関係数(r)はr=0 になりますが,この様な分布であってもデータを良く吟味してみる必要があります.
例えば 図40(右)のように4つの象限を設けたとき,それぞれの象限において相関関係が観察されることもあります.このようなときにはデータの分離を図るべきでしょう.
しかし,これはあくまでも主観的な観察であり2つの標本間の関連性は相関係数(r)と相関の検定によって客観的に記述されなければなりません.
戻る 次へ 目次へ TOPへ