戻る　　　　　次へ　　　　　目次へ

6.3.2.　非直線関係のとき．

相関図において直線関係がみられないときで一方の標本でのデータの分布が正規型で他方が非正規型であれば片対数グラフ用紙などを用いて相関散布図を作成してみます．
もし片対数グラフ用紙上において直線関係が見られればデータの一方を対数変換したのちに相関関係を検討すると良いでしょう．
両方のデータが共に非正規型であれば両対数グラフ用紙などを用いて検討します．
通常，データの分布の関数型と変換式の間には図46のような直線化の関係が知られています．すなわち，それぞれのｘとｙの曲線関係は次の変換によって直線化を試みることができます．

図46　データの分布型と変換式の関係

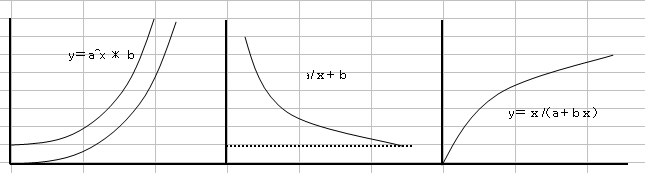
ｙ＝a^x →　Log(y), x 又は Log(x)
ｙ＝a/x → y , 1/x
ｙ＝x/(a+bx) → x/y , x

その他に，Logit-Log 変換などがあります．これは，
Logit ｙ＝Log(y/(1-y) ，　Log ｘ

を Logit ｙ＝ａ・Log ｘ＋ｂ などにあてはめるものでラジオ・イムノアッセイなどでよく用いられています．
この様なデータ変換によっても直線性が得られないときはデータについて質的・量的な問題を検討すべきです．そして，問題がなければ高次回帰への当てはめなどを考えます．
ここでは，ｘに対するｙの回帰において,ｘの２次式を当てはめる手法に次いて説明します．

1) 回帰係数の算出．
２組のｎ個のデータ（Ｘ_i ，Ｙ_i：ｉ＝1,2,･･･,ｎ）から，

Ｙ＝ａ₁ｘ^2＋ａ₂ｘ＋ａ₀

で示される２次回帰式の回帰係数（ａ₁ ，ａ₂）と定数（ａ₀）は，次の連立方程式の解で求められます．

ａ₀ｃ₀＋ａ₁ｃ₁＋ａ₂ｃ₂＝ｚ₀
ａ₀ｃ₁＋ａ₁ｃ₂＋ａ₂ｃ₃＝ｚ₁
ａ₀ｃ₂＋ａ₁ｃ₃＋ａ₂ｃ₄＝ｚ₂

ここで，

ｃ_k＝�狽�_i^k （ｋ＝0,1,2,3,4）
ｚ_k＝�狽�_i・ｘ_i^k （ｋ＝0,1,2 ）

この連立方程式の解によって回帰係数を求めることが出来ます．

筆算で連立方程式式の演算を行う必要はありません。表計算ソフト（エクセルなど）を使えば簡単ですので例題を参考にして下さい。

2) 相関比の計算．
非直線回帰の場合には相関係数(ｒ)を用いることができません．相関係数にかわって相関比,あるいは決定係数(R)と呼ばれる指標を用います．
決定係数(R)は次式で示されます．

R＝SQRT(1−��(y_i−Y^)^2／��(y_i−meanY)^2)

なお，Ｙ^は回帰式より求めた予測値です．また，回帰への当てはめの良さを表す指標として，次の標準誤差(SE)を用いることもあります．

SE＝SQRT(��(y_i−Y^)^2／(ｎ−3)

ただし，ｎ−3 は２次式のときで，３次式のときにはｎ−4 とします．

［例題33］
酵素免疫測定法にてIgE 値を測定し，次の様な標準濃度(IU／L)と吸光度のデータを得ました．

IgE(�])	2	4	8	16	32	64	128
吸光度(Ｙ)	2.7	6.2	12.5	28.8	51.9	92.1	123.8

これから，検量線として使用できる様な回帰式を求めてみましょう．

回帰式は表計算ソフト「エクセルなど」を用いると良いでしょう.
「エクセル」での方法,

「エクセル起動」→「グラフウィザード」→「散布図」→「散布図-値の組を比較します」→「次へ（N）」→「データ範囲（系列で列を選択）」→「完了」

上記の操作で散布図が出来ます。次に,
「散布点を右クリック」→「近似曲線の追加（R）」→「多項式近似（P）」→「オプション」→「グラフに数式を表示する」→OK

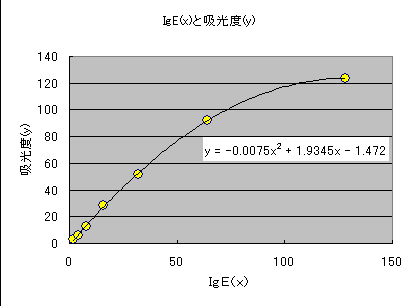
図47 は２次式への当てはめを示したものです．２次回帰式は，
ｙ＝−0.007ｘ２＋1.935ｘ−1.472

で示されます．そして，決定係数は Ｒ＝１ です．

図47　「例題33」における2次曲線の当てはめ

6.3.3.　順位データのとき．
連続量における「相関と回帰」の手法は２つの標本が等分散でその相関関係が直線または直線で近似できるものに適用されました．
この条件が満たされないときで２つの標本が順位尺度のデータであれば，その相関性を「スピルマンの順位相関」によって記述することができます．

1. 相関係数の計算．
２組の対応するｎ個のデータ（Xi，Yi ：ｉ＝1,2,･･･,ｎ）に対して，それぞれの群ごとに順位数を与えます．
例えば図49 の様なデータのとき，

図49　スピルマンの順位相関係数を求める順位系列

ｘ群のデータ(xi)	ｘ1	ｘ2	・・・	ｘi	・・	ｘn
ｘの昇順順位(Rxi)	Ｒx1	Ｒx2	・・・	Ｒxi	・・・	Ｒxn
ｙ群のデータ(yi)	ｙ1	ｙ2	・・・	ｙi	・・・	ｙn
ｙの昇順順位(Ryi)	Ｒy1	Ｒy2	・・・	Ｒyi	・・・	Ｒyn
順位の差(di)	ｄ1	ｄ2	・・・	ｄi	・・・	ｄn
差の２乗(di^2)	ｄ1^2	ｄ2^2	・・・	ｄi^2	・・・	ｄn^2

ｄiの合計 　Ｓ＝�狽�i＝ｄ1＋ｄ2＋・・・＋ｄn

から，スピアマンの順位相関係数（rs）は次式で与えられます．

rs=1-{(6×Ｓ)／(n(n-1)(n+1))}

なお，同じ群に同一順位のデータがあるときには，順位の平均をそれぞれのデータに与えます．
要領は「5.2.　２標本の検定と推定の仕方」でのノンパラメトリック検定と同じです．

［検定の手順］
(1) 検定の問題を明らかにする．
「２組の標本に相関関係があるか？」

(2) 仮説の設定を行う．
帰無仮設（Ｈ0）：ｒ＝0
対立仮設（Ｈ1）：ｒ≠0 （両側検定のとき）

(3) 危険率（100α％）を設定する. 注釈表示

1. 正または負の従属性を検定するときは，片側検定を用いる．

両側検定の有意水準：α

(4) 検定統計量(ｔ0）を計算する．
２組のデータの個数をｎとする順位相関係数（ｒs）の検定統計量（ｔ0）は次式より求めます．

ｔ0＝ｒs* SQRT((n−2)／（1−rs^2）)

　 (5) 統計的判定を行う． 注釈表示

2. ｔ分布表による有意性の検定はデータ数ｎ≧10 に適用する．

　　　 ［両側検定のとき］
ｔ0＜ｔ（n-2,α）ならば，「危険率100α％で相関がない」
ｔ0≧ｔ（n-2,α）ならば，「危険率100α％で相関がある」

なお，ｔ（n-2,α）は表計算ソフト「エクセル」から求めると良いでしょう（例題参照）．

［例題 34］
喘息患者７名について自覚症状の「咳発作回数」と「夜間睡眠障害」の点数づけを行い次の結果を得ました．

咳発作(Ｘ：回／週）	1	2	7	3	5	6	4
睡眠障害(Ｙ：点数)）	0	2	14	6	4	10	2

咳発作回数（ｘ）と睡眠障害点数（ｙ）の間に相関があるか，どうかを調べます．なお，点数は次の基準で与えました．
咳発作１回　　　　：１点／１日 ：１晩中眠れなかった：３点／１日
時々目がさめた　　：２点／１日 ：安眠できた　　　　：０点／１日

スピアマンの順位相関係数(rs)とその有意検定は図50 の順位系列から求めます．

図50　「例題34」の順位系列

ｘ群の順位	1	2	7	3	5	6	4
ｙ群の順位	1	2.5○	7	5	4	6	2.5○
ｄi	0	-0.5	0	-2	1	0	1.5
ｄi^2	0	0.25	0	4	1	0	2.25

S=Σｄi^2=7.5

ｙ群の順位数 2.5（○印）は順位の平均です．
順位の平均はｙ群のデータに同一順位の点数２が２ツあり，その順位が２位と３位になるので，（2＋3）／2＝2.5となります．

順位差の２乗（ｄi^2）の合計はS＝7.5 であるので，順位相関係数（rs）は，

ｒs＝1− (6×7.5)／(7×6×8) ＝0.866

となりまする．そして，検定統計量(ｔ0）は，

ｔ0＝0.866×SQRT{(7−2)/(1−0.866)} ＝3.873

ですので，

t0＝3.873＞ｔ（5,0.05）＝2.571（両側検定，危険率 5％）

から，相関があると云えます．すなわち，
咳発作回数と夜間睡眠障害は関連性があると判断されます．

なお，同一順位があるとき，正確には同一順位に対する補正を次の様に行います．まず，ｘ群とｙ群に同一順位のものが何個あるかを数えます．
そして，その個数をｔ個とすると，Ｔt＝（ｔ^3−ｔ）／12 を同一順位のものすべてについて計算し，その合計（ �狽sｘt ，�狽sｙt ）を求めます．

「例題34」では，
ｘ群のデータには同一順位のものがないので，
�狽sｘt ＝０

ｙ群のデータには同一順位のものが 2.5 で２つあるので，
Ｔｙt ＝（2^3−2）／12＝0.5 ，�狽sｙt＝0.5

となります．ここで，同一順位にたいする相関係数の補正は，
ｒs＝(Ｘ＋Ｙ−Ｓ)／２×SQRT(Ｘ×Ｙ)−�狽syt

なお、
Ｘ＝(ｎ^3−ｎ)／12−�狽sxt
Ｙ＝(ｎ^3−ｎ)／12−�狽syt

となります． 「例題34」では，
Ｘ＝（7^3−7）／12−0＝28 ，Ｙ＝（7^3−7）／12−0.5＝27.5　となります．よって，
ｒｓ＝（28＋27.5−7.5）／（2×SQRT(25×27.5）)＝0.865 となります．
有意性の検定は，このｒs について行えば良いでしょう．

戻る     次へ      目次へ     TOPへ