- 共通の分布は同時分布としてf(x,y)で表す.また,濃度(x)で蛍光強度(y)を反復して測定すればランダムな誤差により,ある平均値を中心にバラツキが見られるはずである.
よって,その平均値は濃度を(X)とする条件付きのもとでのyの分布であり,これを条件付分布f(y/x)と呼ぶ. - 血圧の例では最高血圧も最低血圧も同じ mmHg であるがデータによっては,例えば ㎏ ,㎝ ,㎎ ,Ug など単位の異なるものがある.標準化によって単位と無関係になった変量を標準化変量と云う.
6章 2標本の関連性をみる
2つの標本の関連性は1標本のときと同じように,2つの標本についてそれぞれの標本の性質を記述することから始めます.
標本の性質は平均値と標準偏差,そして度数分布などの代表的な統計量で記述します.これは標本からの情報をもとに,母集団への一般化を図るものであり,2つの標本の関連性をみるときも同じです.
ただ関連性の記述は一方の群(A群のデータ)が大きくなれば,他方の群(B群のデータ)も平均して大きくなり,反対に小さくなれば平均して小さくなるようなA群とB群の関係や,あるいはA群のデータが大きくまたは小さくなっても,B群のデータが平均して大きくも小さくもならないような関係を示すものでなければなりません.
それは母集団において「相関関係がある」か,あるいは「相関関係がない」かの問題だけでなく,相関関係の度合やその度合の強さを示すものでなければなりません.
ここでは相関とは何かについて考えてみたいと思います.
次の2組のデータはある物質の濃度(x)と,その蛍光強度(y)の関係を示しています.
| 濃 度(x) | 0 , 5 , 10 , 15 , 20 |
| 蛍光強度(y) | 5 , 31.25 , 57.5 , 83.75 , 110 |
この2組のデータから濃度(x)と蛍光強度(y)の比例関係を図26 のようなxとyの共通分布で示します.これを私達は医学実験で用いると,検量線と云っています. 注釈表示
図26 濃度(x)と蛍光強度(y)の関係
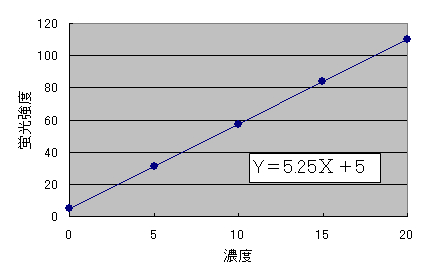
一般に2組(x ,y)のn個のデータが与えられたとき,xとyの相互間の関数的な関係,すなわちxに対するyの回帰直線(y=ax+b)を求めることを相関分析と云います.
これに対し,xの値を与えてyの値を予測することを回帰分析と云います.
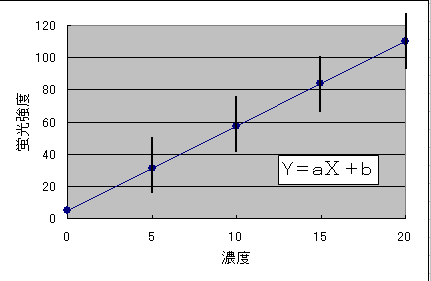
例えば,図26 の濃度(x)と蛍光強度(y)の関係は,図27 のように各濃度(xi)をもつyの期待値 E[y/x],分散の期待値 V[y/x] の直線性の仮定で示すことが出来ます.
図26 のようににxの変化に対するyの変化が直線的であれば,明らかに強い関連性のあることが分かるでしょう.
図27 相関関係における期待値
そして,この関連性がy=5.25x+5 の1次式(回帰直線)で表現できることも容易に理解できるでしょう.
しかし,実際にはこれほどはっきりした相関は少ないと思います.次の例を見てみましょう.
| 希釈倍率(x) | 1/2 , 1/4 , 1/8 , 1/16 , 1/32 |
| 蛍光強度(y) | 34 , 106 , 109 , 58 , 20 |
希釈倍率(x)が大きくなるほど蛍光強度(y)は減少しています.
この関係は図28 のようにマイナスの係数を持つ1次式 y=-3.8x+130.5 で示されます.
図28 希釈倍率(x)と蛍光強度(y)の関係
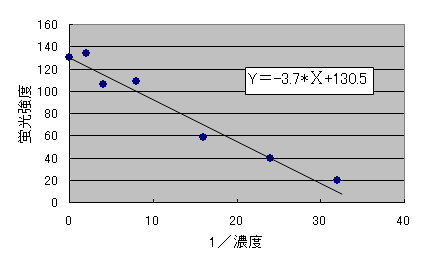
図28 の分布は回帰直線の両側にバラツキがみられ直線上に並んだ図26 の関連性よりも弱いことが分かります.
実際のデータでは大なり小なり,この様なバラツキが見られるもので回帰直線の勾配(a)および切片(b)は回帰直線とx,yのプロット点(●印)の距離(d)の2乗和が最小になるように最小2乗法によって求めます.
これを直線への当てはめと云います.
この様に,データを平面座標上にプロットして相関散布図を作ったり回帰直線への当てはめを行うことによって,2標本間の関連性を視覚的にとらえることが出来るようになります.
次に,関連性の度合を表すのに良く用いられる相関係数について考えてみましょう.
図29 の相関散布図はxとyを軸として,その交点を18 個のプロット点(●印)が対等の数(6:6 と 3:3)になるようにに定めたものです.
図29 相関散布図の各象限と相関関係
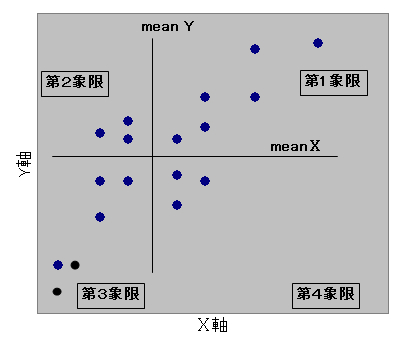
この散布図をみると第1象限と第3象限に最も多くのプロット点があります.第2象限と第4象限には僅かのプロット点しかありません.
第1と第3象限にプロット点があれば,正の相関
第2と第4象限にプロット点があれば,負の相関
を表わしています.したがって,図29の相関散布図は多くのプロット点が第1と第3象限に分布しているので正の相関を表します.
もし,多数のプロット点が第2と第4象限に分布しておれば負の相関を,また各象限に一様にプロット点が分散しておれば,「0」に近い相関を表します.
各象限単位での平均値(meanX,meanY)からの偏差をdxi,dyi とするとき相関係数(r)は次により求められます.
(1)平均値(meanX,meanY)からの偏差を求める.
dxi=Xi-meanX , dyi=Yi-meanY (i=1,2,・・,n )
これは各データ(Xi ,Yi)を平均値(meanX ,meanY)を中心とする原点に移すことになります.
(2)偏差の平方和(変動)と積和(共変動)を求める.
Sxx=∑Xi2 =∑(Xi-meanX)2
Syy=∑Yi2 =∑(Yi-meanY)2
Sxy=∑Xi*Yi=∑ (Xi-meanX)(Yi-meanY)
(3)分散・共分散と標準偏差を求める.
Vx=Sxx/n , Vy=Syy/n , Vxy=Sxy/n
SDx=SQRT(Vx) ,SDy=SQRT(Vy)
(4)相関係数(r)を求める.
r=Vxy/(SDx*SDy)
すなわち,相関係数(r)は,
(xとyの共分散)/{(xの標準偏差)×(yの標準偏差)}
と表すこたができます.
なお,共分散(Vxy)を標準偏差(SDx ,SDy)で割ることは2章で述べた標準化と同じことで,xとyの単位が異なっていても同一の尺度となります.
以上は私達の医学的実験でよく用いられる検量線を例として説明しました.
次に,これを「最高血圧の高い者は,最低血圧も高いか?」と云う問題について考えてみたいと思います.10 名の平均的な最高血圧(X)と最低血圧(Y)が次のようでであったとします.
| X | 110 , 120 , 130 , 140 , 150 , 160 , 170 , 180 , 190 , 200 |
| Y | 78 , 73 , 75 , 80 , 90 , 95 , 100 , 94 , 106 , 110 |
最高血圧の平均値は meanX=155.0 mmHg
最低血圧の平均値は meanY= 90.1 mmHg
その相関散布図を図30 に示します.図30 において,XとYが相関散布図の原点にくるようにします.すなわち,
meanX= 0 , meanY= 0
となるように,
dx=Xi-meanX dy=Yi-meanY
から求めた次の値をプロットし図31 の変換変量散布図を作ります.
図30 例題での最高血圧と最低血圧のし有漢散布図
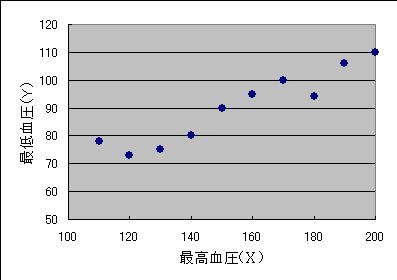
図31 最高血圧と最低血圧における変換変量の散布図
変換散布図を見るとプロットの多くはは第1と第3象限にあり正の相関を示すことが分かるでしょう.
次に,XとYの単位に無関係になるように,dx , dy を標準偏差 SDx ,SDy で除し,全てのデータを標準化します.
標準化したデーターの標準化変量(Zx,Zy)は次のようになります.
注釈表示
| Zx | -1.57 , -1.22 , -0.87 , -0.52 , -0.17 , 0.17 , 0.52 , 0.87 , 1.22 , 1.57 | (/tr>
| Zy | -0.927 , -1.37 , -1.21 , -0.81 , -0.01 , 0.39 , 0.79 , 0.31 , 1.28 , 1.60 |
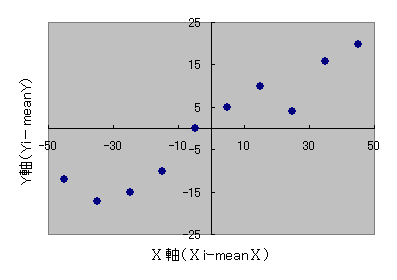
標準化変量の散布図は図32 の様に45°の角度で原点を通る直線の周りに散布することが分かります.
図32 最低血圧と最高血圧における標準化変量の散布図
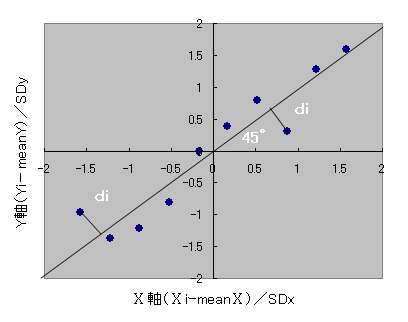
ここで直線からの垂直な距離(di)の2乗和,すなわち,
Td= (d1^2 + d2^2 +・・・・・+d10^2)/10
において,Tdが小さいほど直線への当てはめが良いと云えます.これは標本間の相関が強いことを示すものです.
最高血圧と最低血圧の相関係数(r)は,
Vxy=(dx1・dy1+dx2・dy2+・・・・・+dx10・dy10)=339.5
よって,
r=Vxy/(SDx・SDy)=339.5/(28.73×12.47)=0.948
を得ます.
相関係数(r)は,その値が正または負に係わらず十分に大きいとき直線へのあてはめが良く,その値が小さいとき直線への当てはめが悪いことを示しています.
この様に相関係数(r)は相関の強さの度合を示す測度としてより2変量間の直線関係を示す尺度と考えた方が良いでしょう.何故なら,ここでの相関係数(r)は2変量間の直線関係以外は表現できないからです.
このことは2変量の分布が正規分布であることを前提とします.もし,いずれか一方の変量が非正規型であれば,これを適当なデータ変換によって正規化を図り正規分布としてから相関係数を求める必要があります.
しかし,2変量間の関連性については直線関係のデータに限ることはありません.2変量間の相関散布図を参考に必要に応じて重相関分析「7章(8.1.)」,順位相関分析「6章(7.8.)」の適用も検討されるべきでしょう.
次に,xに対するyの回帰からxの値を与えてyの値を推定もしくは予測する回帰分析について考えてみましょう.
回帰分析では通常xの値に対するyの分布を考えるところから x を独立(説明)変数,yを従属(目的)変数と云います.
例えば,図33 の最高血圧(x)と最低血圧(y)の相関関係から求めた回帰式は
y=0.412x+ 26.32
です.
この式にxを代入することによってyの値(最低血圧)を推定することが出来ます.これとは逆にyに対するxの回帰式を求めておけば,yの値を与えてxの値(最高血圧)を推定することが出来きます.
図33 最高血圧と最低血圧における回帰式
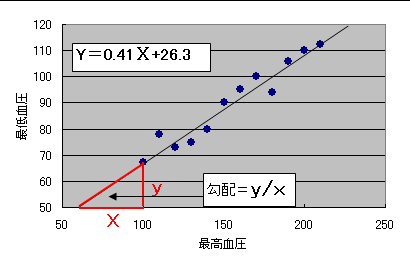
医学実験などで用いられる検量線は,例えば,濃度(X)と蛍光強度(y)に対する回帰直線から蛍光強度(y)を与えて濃度(X)を求めることが多いものです.
これを線形校正と云い検量線として逆推定するときはこの回帰直線を「校正直線」と呼びます.
このような逆推定はいろいろな検量線に関する問題を提起するものですが,統計学的にはxに対するyの回帰式とyに対するxの回帰式の両方を求めておく方がよいと思います.
回帰に関する問題としてx軸とy軸の両軸の誤差を考慮することも大切ですが,ここでは専門的であり混乱を招く恐れがあるので取り上げません.
なお,回帰式を Y=aX+b で示すとき,その勾配(a)と切片(b)は次式より求めます.
a=Sxy/Sxx=(XとYの共変動)/Xの変動 =(XとYの共分散)/Xの分散
b=meanY-aX
よって,血圧の例では,
a=339.5/825.0=0.4115 b=90.1-0.4115*155=26.32
となります.したがって回帰式は,
Y=0.412X+ 26.32
となります.さらに,
回帰分析においては,血圧の散布図のように回帰直線の両側に各プロット点が散布しているときは,その誤差の範囲も示す必要があります.
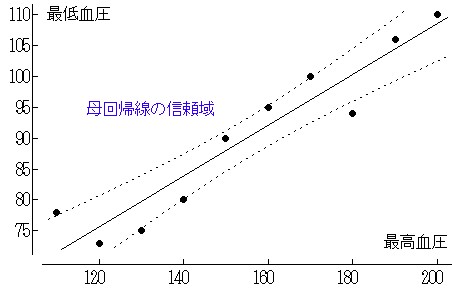
これを信頼区間と云い図34 の2つの信頼曲線で示されます.
2つの信頼区間は,
(a) 母回帰線の信頼区間
(b) 予測値の信頼区間
であり,ある特定の値(X0) を与えたとき次式で示されます.
(a)母回帰線100(1-α)%の信頼区間
Y±t(n-2,α)SQRT{Ve(1/n+(X0-meanX)/Sxx}
図34 最高血圧と最低血圧における2つの信頼曲線
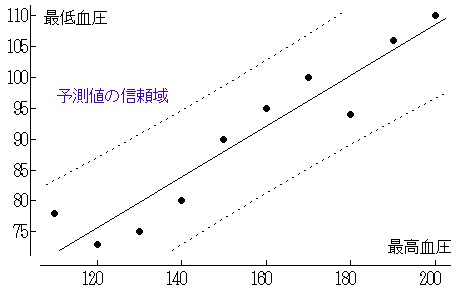
(b)予測値100(1-α)%の信頼区間
Y±t(n-2,α)SQRT{Ve(1+1/n+(X0-meanX)/Sxx}
ここで,残差分散(Ve)は,
Ve=Se/(n-2)
Se(残差平方和)=Syy-Sxy/Sxx
なお,t(n-2 , α)は 表計算ソフト「エクセル」から求めると良いでしょう.
(C)母回帰係数,勾配(a)の信頼区間
a±t(n-2,α)SQRT(Ve/Sxx)
(d) 母回帰係数,切片(b)の信頼区間
b±t(n-2,α)SQRT{Ve{1/n+meanX/Sxx}}
この様に標本から得られたデータをもとに母集団での相関と回帰を考えることは,再々云っているように統計をとる目的の1つなのです.
したがって,2標本の関連性においても相関の検定を行う必要があります.
それは,母相関係数(ρ)がゼロ(ρ=0)かどうかのの問題であり次のようにします.
(5)仮説を立てる.
帰無仮説(H0):ρ=0
対立仮説(H1):ρ≠0
(6)検定統計量(t0)を求める.
t0=r*SQRT(n-2)/(1-r)
(7)統計的判定を行う.
t0≧t(n-2)ならば,「危険率100α%で有意である」
すなわち,母相関係数(ρ)はゼロでない(ρ≠0)と云えます.
相関係数(ρ=0)の検定は,母相関係数がゼロであるかどうかの検定であり相関の度合を問題にしているのではありません.
したがって,母相関係数がρ≠0 を理由に「相関がある」と結論することは出来ません.この点から云えば5章の有意性の検定のように有効とは云えないでしょう.
相関係数の有効性は線形回帰において意味を持つと云えます.したがって,
母集団での相関関係を問題にするときは,母相関係数(ρ)の検定と同時に前記の回帰直線の推定から判断する方が良いと思います.
ここでは独立変数が1つの場合,すなわち,Y=aX+bで示される相関と回帰の問題について述べました.
相関及び相関回帰は表計算ソフト「エクセル」の
「ツール(T)」→「分析ツール(D)」→「相関」及び「回帰分析」
を利用すれば良いでしょう。
戻る 次へ 目次へ TOPへ