- 標本の数(n)がn≧9のとき,検定統計量の分布が KAI2 分布するので,ここでの検定統計量(Q)を用いることができる.
n<9のとき,ここでの検定統計量(Q)を用いて検定できないので注意されたい。 - ここでの検定は要因(B)間の検定であり,標本(A)間の検定はできないので注意されたい.
- データの順位変換において,A群のデータに同じ順位のものがあるとき順位の平均をそのデータの順位とする.
5.3.5. 対応のあるとき(フリードマンの順位検定)
[一般形式]
[検定の手順]
1. 検定の問題を明かにする.
2. 仮説の設定を行う.
3. 危険率(100α%)を設定する.
4. 検定統計量(Q)を計算する.
注釈表示
2元配置分散分析では等分散性と正規性の仮定のもとに,少なくとも間隔尺度で測られたデータが検定の対象になります.
しかし,標本が非正規性であったり,因子での水準差がありすぎたり,あるいは離散量とか順位尺度のデータのときは,ここでのフリードマン(Friedman)の順位検定を用いると良いでしょう.
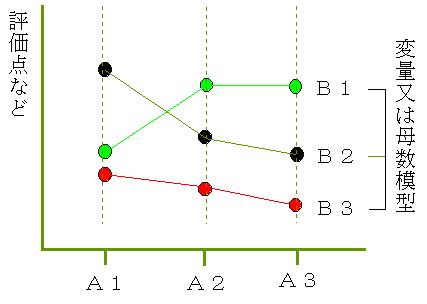
.....「対象とする要因間に有意な差があるか?」
.....帰無仮設(H0):μ1j=μ2j=・・・=μnj.
.....対立仮設(H1):μ1j≠μ2j≠・・・≠μnj.
.........................(両側検定になる)
.....両側検定の有意水準:α
.....2つの要因からなる2因子のデータを,
.....n=標本(A)の行数
.....m=要因(B)の列数
.....Rj=各水準における順位の部分和(j=1,2,・・・,n)
とするとき,データの符号化と順位変換のために,データをひとまとめにして,各標本ごとに 表41 のよな昇順順位系列をつくります. 注釈表示
| 標本(A/B) | B1 | B2 | ・・ | Bj | ・・ | Bm |
| A1 | R11 | R12 | ・・ | R1j | ・・ | R1m |
| A2 | R21 | R22 | ・・ | R2j | ・・ | R2m |
| Ai | Ri1 | Ri2 | ・・ | Rij | ・・ | Rim |
| An | Rn1 | Rn2 | ・・ | Rnj | ・・ | Rn |
| 順位部分和 | R.1 | R.2 | ・・ | R.j | ・・ | R.m |
次により,順位の平均値を求めます.
Sj=ΣRij/n
そして、分散を求めます.
V=ΣΣ(Rij−(m+1)/2)2
これにより,フリードマンの検定統計量(Q)は,
Q=n2*(n−1)/V *Σ(Sj−(m+1)/2)2
となります。
5. 統計的判定を行う.
Q<KAI2(m−1,α)ならば,「危険率100αで有意な差がない」
Q≧KAI2(m−1,α)ならば,「危険率100αで有意な差がある」
なお,KAI2(m-1,α)は 表計算ソフト「エクセル」)から求めると良いでしょう.
求め方は「例題」を参考にして下さい。
[例題29]
気管支喘息患者の病態別の血清IgE値が,表42 ように 10 ランクの点数で与えられているとき,フリードマンの順位検定によって, 病態間に有意な差があるかどうかを検定してみます.
| 標本(A)/病態(B) | アトピー型(B1) | 混合型(B2) | 感染型(B3) |
| A1 | 9 | 7 | 3 |
| A2 | 10 | 6 | 3 |
| A3 | 6 | 7 | 3 |
| A4 | 5 | 6 | 3 |
| A5 | 8 | 4 | 2 |
| A6 | 7 | 2○ | 2○ |
| 標本(A)/病態(B) | アトピー型(B1) | 混合型(B2) | 感染型(B3) |
| A1 | 3 | 2 | 1 |
| A2 | 3 | 2 | 1 |
| A3 | 2 | 3 | 1 |
| A4 | 2 | 3 | 1 |
| A5 | 3 | 2 | 1 |
| A6 | 3 | 1.5 | 1.5 |
| 順位部分和 | R=16 | R=13.5 | R=6.5 |
表43 から検定統計量(Q)を求めますが,計算は表計算ソフト「エクセル」を使うと便利でしょう。
ここでは,「エクセル」による計算過程を示します。
フリードマンの検定統計量は
Q=8.4348
ここで,KAI2分布表から,
KAI2(m-1,α)=KAI2(2,0.05)=5.9915
であるので,
Q=8.4348>KAI2(2,0.05)=5.9915(両側検定,危険率 5%)
から,病態によって IgE に有意な差があると云えます.KAI2値は表計算ソフト「エクセル」の関数から求めます。
エクセル関数 CHIINT(0.05, 2)=5.9915
検定の結果,帰無仮説(H0)は棄却され「有意な差がある」との結果を得ました.しかし,どの要因間(列水準)に差があるかは分かりません。
どの要因間に差があるかは多重比較によって判断します.
「例題29」ではアトピー型(B1)と感染型(B3)の間にのみ有意差が認められました.
多重比較については,「5.3.3. 多群間の平均値を比較する」で説明しましたが,ここでもこれらを利用してた群間の比較が出来ます.
戻る 次へ 目次へ TOPへ