戻る　　　　　次へ　　　　　目次へ

5.3.　多標本の検定と推定の仕方.
3つ以上の標本間でその平均値の差の検定を行うとき、2つの標本を一対として個々に ｔ検定「5.2.　2標本の検定と推定の仕方（5.2.　平均値のとき）」を行っているのが、 医学などでのｔ検定でときどき見受けられます。
これは、例えばＡ・Ｂ・Ｃの標本において、医学的な経験ないし知識によってＡとＢ、あるいはＢとＣの平均値に有意な差のあることが検定以前に予想できる場合の限って使用すべきでしょう。
この様な検定は片側仮説に対する探索的な検定であって、その有意性を確認するだけのために用いるものです。
もし、探索的な検定でなければ「分散分析」のＦ検定の適用を考えるべきです。ここでは分散分析の手法として、
�@多標本での「対応のない平均値の差の検定」として、1元配置分散分析。
�A多標本での「対応のある平均値の差の検定」として、2元配置分散分析。

について説明します。
なお、分散分析では等分散性と正規性の仮定のもとで検定を行うので、その仮定が困難なものは「ノンパラメトリック検定」を適用するようにします。 注釈表示

分散分析の等分散性と正規性はデータ数が同じであればそれほど厳密に考えることはない

5.3.1　対応のないとき（1元配置分散分析）
2つの標本間における平均値の差の検定ではｔ検定を用いました。3つ以上のパラメトリック検定では1元配置分散分析を用いて検定します。

[一般形式]

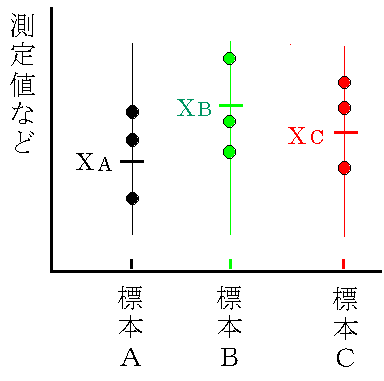
［検定の手順］
�@検定の問題を明かにする．
「標本間の平均値に差があるか？」

�A仮説の設定を行う．
帰無仮設（Ｈ0）：μ1＝μ2＝・・・＝μk
対立仮設（Ｈ1）：μ1≠μ2≠・・・≠μk 注釈表示

分散分析でのＦ検定ではＦ比の値が１因子の水準間に有意差のあること，すなわち水準間分散＞水準内分散が仮定される片側検定であるが両側仮設と同等の考えて良い．

�B危険率（100α％）を設定する.
片側検定の有意水準：α

�C検定統計量(F_A)を計算する．
多群のデータを
ｋ＝標本の数(水準数)
n_i＝各水準のデータの個数
Ｎ＝全データの個数
�]_ij＝データ
T＝全データの合計
TA_i＝各水準のデータの合計(ｉ＝1,2,･･･,ｋ : ｊ＝1,2,･･･,ｎi)とするとき,１元配置分散分析は表28の様な記号で表わされます．
　 　

表28 一元配置の記号

因子(k水準)	1.....2..・・ .j...・・...n	計
Ａ1	Ｘ11　Ｘ12 ・・ Ｘ1j ・・ Ｘ1n1	ＴA1
Ａ2	Ｘ21　Ｘ22 ・・ Ｘ2j ・・ Ｘ2n2	ＴA2
:	:	:
Ａi	Ｘi1　Ｘi2 ・・ Ｘij ・・ Ｘini	ＴAi
:	:	:
Ａk	Ｘk1　Ｘk2 ・・ Ｘkj ・・ Ｘknk	ＴAk
総和	Ｎ＝ｎ1＋ｎ2＋・・＋ｎk	Ｔ

表28 から各平方和(変動)は,次により求めます． 　
全平方和(全変動) : ＳT＝�這狽w−Ｔ／Ｎ
級間平方和(級間変動)：ＳA＝�狽s／ｎ−Ｔ／Ｎ
誤差平方和(級内変動)：ＳE＝ＳT−ＳA 　

これらの平方和を 表29 の1元配置分散分析表にまとめます．

表29 1元配置分散分析表

要因	平方和(S)	自由度(DF)	分散(V)	F比
因子(A) 誤差(E)	SA SE	DFA=k-1 DFE=N-k	VA=SA/DFA VE=SE/DFE	FA＝VA/VE
全体(T)	ST	DFT=N-1	..	..

表29の１元配置分散分析表から検定統計量はＦ比欄のＦAとなります．　 　　　

�D統計的判定を行う．
ＦA＜Ｆ（DFA,DFE,α）ならば，「危険率100α％で有意な差がない」
ＦA≧Ｆ（DFA,DFE,α）ならば，「危険率100α％で有意な差がある」

なお，Ｆ(DFA,DFE,α)は表計算ソフト（エクセル）から求めます．
求め方は「例題24」を参考にして下さい。

�E100(1-α)％の信頼限界を求める．
上限値：
ＴA_i／ｎ_i＋ｔ(DF,α／2)×SQRT(ＶE／ｎ) 　　

下限値：
ＴA_i／ｎ_i−ｔ(DF,α／2)×SQRT(ＶE／ｎ)

但し，各水準の分散が等しいときに限り求めることができます．

［例題24］
収縮期血圧について3標本(Ａ・Ｂ・Ｃ)の年代別における平均値と標準偏差が与えられているとき，そのデータをもとに分散分析を行ってみましょう．
各標本(水準)での平均値(Ｘ^bar)，標準偏差(ｓ)，データの個数(ｎ)は，次の通りです．
Ｘ_A^bar＝127.4 ，ｓ_A＝17.2 ，ｎ_A＝50
Ｘ_B^bar＝130.3 ，ｓ_B＝19.7 ，ｎ_B＝50
Ｘ_C^bar＝143.0 ，ｓ_C＝26.8 ，ｎ_C＝50

例題では各標本(水準)での平均値(Ｘ_i^bar)と標準偏差(ｓ_i)しか与えられていません．
しかし，分散分析でのＦ検定は級内変動に対する級間変動の割合を示すものですので，
全標本での全変動は，

�這�(Ｘ_ij−Ｘ^bar)²＝�這�(Ｘ_ij−Ｘ_i^bar)²＋�狽�_i(Ｘ_i^bar−Ｘ^bar)²　

で表されます．ここで、

�這�(Ｘ_ij−Ｘ_i^bar)²を第1項、
�狽�_i(Ｘ_i^bar−Ｘ^bar)²を第2項

とするなら、
第１項は級内変動(Ｓi)であり,Ｓi＝(ｎ_i−1)×ｓ_i²に等しいものです．
したがって,例題での各標本(水準)での平均値（Ｘ_i^bar）および標準偏差（ｓ_i）から，
総平均（Ｘ^bar）は，

Ｘ^bar＝�狽�_iＸ^bar／Ｎ
(Ｎ＝ｎ_A+ｎ_B+ｎ_C）

から求められます．
以下に例題での計算手順を示します．

総平均（Ｘ^bar）：
Ｘ^bar＝50×(127.4＋130.3＋143)／150＝133.57

級内変動（Ｓ_E）：
Ｓ_A＝（ｎ_A−1)ｓ_A²＝（50−1）×17.2^2＝14496.16
Ｓ_B＝（ｎ_B−1)ｓ_B²＝（50−1）×19.7^2＝19016.41
Ｓ_C＝（ｎ_C−1)ｓ_C²＝（50−1）×26.8^2＝35193.76
計　　Ｓ_E＝68706.33

級間変動（Ｓ_A）：
Ｓ_A＝50×（127.4−133.57）^2＝1903.445
Ｓ_B＝50×（130.3−133.57）^2＝ 534.645
Ｓ_C＝50×（143.0−133.57）^2＝4446.245
計 Ｓ＝6884.335

これらを１元配置分散分析表にまとめると表30 のようになります．

表30　「例題24」の１元配置分散分析表

要因	平方和(S)	自由度(DF)	分散(V)	F比
因子(A) 誤差(E)	ＳA＝6884.335 ＳE＝68706.33	DFA=3-1 DFE=150-3	VA=3442.17 VE=467.39	FA＝7.365
全体(T)	ＳT＝75590.665	DFT=150-1	..	..

ここで，Ｆ分布の上側パーセント点は表計算ソフト・エクセル（関数式）から，
ＦA(DFA,DFE,α)＝Ｆ(2,147,0.05）＝3.0576

ですので，
ＦA＝7.365＞Ｆ(2,147,0.05)＝ 3.0576（危険率 5％）

から，各標本での平均値に有意な差があると云えます．

すなわち，年代(３標本)によって平均値の異なる標本(水準)があると判断されます．
なお,標本(Ａ)と標本(Ｂ)が等分散とすれば,その95％信頼限界は次のようになります．

標本(Ａ）：
Ｘ_A^bar±ｔ(DFE,0.05／2)・SQRT(ＶE／ｎ_A)＝127.4±1.9762×SQRT(467.39／50)＝127.4±6.042 　

標本(Ｂ）
Ｘ_B^bar±ｔ(DFE,0.05／2)・SQRT(Ｖ／ｎ_B)＝130.3±1.9762×SQRT(467.39／50)＝130.3±6.042

なお，ｔ(DFE,0.05／2)は表計算ソフト・エクセル（関数式）から求めます．

以上は表計算ソフト「エクセル」を用いて計算することが出来ます。

関数式による方法

［例題25］気管支喘息患者の病態別の血清ＩgＥ値（IU/L）を次に示します．

アトピー型	混合型	感染型
850	840	260
600	540	200
710	560	100
900	400	210
550	830	300

ここで，
標本の数:ｋ ＝3
各データの個数(水準数):ｎi＝5,5,5（i＝1,2,3）
総データの個数:Ｎ＝5＋5＋5＝15

です．以上から，
表計算ソフト（エクセル）の「分析ツール」(Sheet名「分析ツール」)を用いた方法を次に示します。

「分析ツールによる方法」
「ツール(T)」→「分析ツール(D)」→「分散分析：1元配置」

以上から，検定統計量（ＦA）は，

ＦA＝ＶA／ＶE＝16.67

となります．
ここで，自由度DFA＝ｋ−1＝ 2 ，DFE＝Ｎ−ｋ＝ 12 ，有意水準 α＝0.05 に対するＦ分布のパーセント点は，
Ｆ(2,12,0.05）＝3.8853 ですので，
Ｆ＝16.67＞Ｆ(2,12,0.05)＝3.8853（危険率 5％）

から，標本間の平均値に有意な差があると云えます．

誤用を避けるために！
血清IgE 値は非正規分布であることが知られています．一元配置分散分析では正規性、等分散の仮定のもとに検定が行われます。
したがって、血清IgE 値は自然対数変換をおこない正規分布近似とする必要があります。
自然対数変換値による結果は次の通りです．

自然対数変換値

アトピー型	混合型	感染型
6.745	6.733	5.561
6.397	6.292	5.298
6.565	6.328	4.605
6.802	5.991	5.347
6.310	6.721	5.704

分散分析表

要因	自由度	平方和	平均平方	F値	ｐ値
Ln(IgE)	2	4.741	2.37	21.956	<0.0001
誤差	12	1.296	0.108	...	...
全体(修正済み)	14	6.036	...	...	...

この様なＦ検定は級内変動に対する級間変動の割合によって決まるものであり,その有意差を示す標本間を特定するものではありません．
したがって,有意差を示す標本間を特定しなければＦ検定をした意味がないと云えます．
これについては，次の「5.3.2. 多群関の平均値を比較するとき」で説明しますので,ここでは１元配置分散分析の仕方を知っておいて欲しいと思います．

戻る     次へ      目次へ     TOPへ