- 片側検定で対立仮説(H1)がσA>σBのときは検定統計量(F1)をσB>σAのときは検定統計量(F2)を用いる。
- 分散比の検定において有意、すなわち「バラツキが異なる」と判断されたとき、それは「同一の母集団からとられたデータとは云えない」と結論ずける前に、
a)飛び離れた異常データがないか?
b)標本間のデータ数が違い過ぎていないか?
c)データの分布が正規分布から、かけ離れ過ぎていないか?
などを検討すべきである。 - 分散比の 95%信頼限界は、F分布の下側(α=0.975)がF分布表にないので、F(φA,φB,α)=1/F(φB,φA,α)の関係を利用する。
2つの母集団からとられた2つの標本であっても,その平均値を異にする場合とか,平均値は同じでもその分布の状態(バラツキ)が異なる場合もあります.
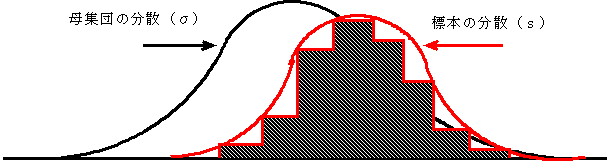
実際の医学統計では,2つの母集団での母分散(σ2)が未知のことが多く,標本のバラツキからその標本がとられた母集団のバラツキを検定したり推定することの方が多いと云えます.
5.2.1. 分散比のとき.
2つの標本から2つの母集団における母分散(σ2)が等しいか,あるいは異なっているかを検定します.
これは平均値に関する検定をおこなうときに,最初におこなう大切な手法です.
通常,医学において2つの標本の検定を行うとき,
- 「平均値の差」だけを問題にしているのか?
- 「バラツキの差」を問題にしているのか ?
- 「平均値の差」と「バラツキの差」の両方を問題にしているのか?
を考えなければなりません.
[検定の手順]
(1)検定の問題を明らかにする.
.....「2つの標本のバラツキは等しいか?」
(2)仮設の設定を行う.
.....帰無仮説(H0):σA2=σB2
.....対立仮説(H1):σA2≠σB2 (両側検定のとき)
.....対立仮説(H1):σA2>σB2 またはσA2<σB2 (片側検定のとき)
(3)危険率(100α%)を設定する.
両側検定の有意水準:α/2
片側検定の有意水準:α
検定統計量(F1,F2)を計算する. 注釈表示
.....VA≧VB ならば,F1=VA/VB
.....VB>VA ならば,F2=VB/VA
ここで、VA=A群の標本分散 :VB=B群の標本分散 である。
統計的判定を行う. 注釈表示
[両側検定のとき]
.....F1<F(φA,φB,α/2)または、F2<F(φB,φA,α/2)ならば、
..... 「危険率100α%でバラツキに差がない」
.....F1≧F(φA,φB,α/2)または、F2≧F(φB,φA,α/2)ならば、
.....「危険率100α%でバラツキに差がある」
[片側検定のとき]
.....F1≧F(φA,φB,α/2)または、F2≧(φB,φA,α/2) ならば、
.....「危険率100α%でバラツキ大きい(小さい)」
但し、φA=nA−1、φB=nB−1(nA=A群のデータの個数、nB=B群のデータ個数)である。
なお,F(φA,φB,α/2)、F(φB,φA,α/2 )はF分布表「表計算ソフト(エクセル)」から求めます。
求め方は「例題」を参考にして下さい。
100(1−α)% の信頼限界を求める。
上限値:
.....F(φB,φA,α/2)× (VA/VB)
下限値:
.....(VA/VB)/F(φA,φB,α/2)
[例題19]
ある企業検診での年代別の収縮期血圧が次のようであった。それぞれの年代で血圧のバラツキに差があると云えるか検定してみます。
(A)は年齢 30〜39才、30名の血圧の平均値XbarA=122.5 mmHg、標準偏差sA= 10.85 mmHg である。
(B)は年齢 40〜49才、20名の血圧の平均値XbarB=133.4 mmHg、標準偏差sB= 12.24 mmHg である。
(C)は年齢 50〜59才、10名の血圧の平均値XbarC=131.0 mmHg、標準偏差sC= 21.4 mmHg である。
最初に各標本間の分散比の検定を行います。
(A)と(B)のバラツキは SA<SBですので検定統計量(F2)を用います。
F2=SB2/SA2=12.24^2/10.85^2=149.82/117.72=1.273
したがって、
F2=1.273<F(19 , 29 , 0.05/2)= 2.231(両側検定、危険率5%)
から、有意な差がないと云えます。すなわち、(A)と(B)の分散は等しいと判断されます。
F(19,29,0.025)の値は表計算ソフト(エクセル)から次により求めます。
「挿入(T)」→「関数(F)」→「統計」→「FINV」→{(確率=0.025,自由度1=19,自由度2=29)}
次に、
(B)と(C)の検定統計量(F2)は,
F2=SC2/SB2=21.4^2/12.24^2=457.96/149.82=3.057
したがって、
F2=3.057>F(9 , 19 , 0.05/2)= 2.880 (両側検定、危険率5%)
から、有意な差があると云えます。すなわち、(B)と(C)の分散は異なると判断されます。
F(9,19,0.025)の値は表計算ソフト(エクセル)から次により求めます。
「挿入(T)」→「関数(F)」→「統計」→「FINV」→{(確率=0.025,自由度1=9,自由度2=19)}
分散比の推定は(A・B)と(C)は等分散でないので推定できません。ここでは、(A)と(B)の母分散比を推定してみましょう。
95%信頼限界3)は次の通りです。
上限値:
(SB2/SA2)×F(φA , φB , 0.05/2)=(149.82/ 117.72)×F(29 , 19 , 0.025)
=1.273×2.402=3.058
下限値:
(SB2/SA2)×1/F(φB , φA , 0.025)= (149.82/117.72)×1/F(29 , 19 , 0.025)
=1.273×1/2.231=0.571
したがって、母分散比は、
0.571≦σB2/σA2≦3.058(分散 )
0.76 ≦σB /σA ≦1.75(標準偏差)
の範囲と推定されるので、母集団での(B)の標準偏差は大体(A)の1.25 倍程度でしょう。
F(9,19,0.025)の値は表計算ソフト(エクセル)から次により求めます。
「挿入(T)」→「関数(F)」→「統計」→「FINV」→{(確率=0.025,自由度=29,自由度2=19)}
{(確率=0.025,自由度=19,自由度2=29)}