- データはある集団から(母集団を意味しているが,これについては後に述べる)から,無作意・確率的(ランダム性を意味する)収集されもので,確率変数と見なされ統計的には確率変数のこと変量と呼ぶ.
- 定性的データに1か0の数値を与えたものを数量化データと云う.
- 尺度とは,データの特性に対し,数値を割り当てる基準となるもので,通常,間隔尺度(比尺度を含む),名義尺度(分類尺度),順位尺度などに分類される.しかし,絶対的なものではないので,統計をとる目的によって使いわければ良い.通常,離散型データのうちでも,相互になんの関係もないデータを名義尺度のデータと,ある一定の順序があるものを順位尺度のデータと呼んでいる.
戻る 次へ 目次へ
1章 データを整理する
通常,私達が統計をとるときは,ある目的を持ってデータを集めます.ときには,収集し蓄えられてデータから偶然に,ある種の情報をデータの中に見いだすこともあります.仮に,その情報がいままで学習したことのないもので,私達の理解の範囲を越えていたとしても,その後の多くの学習と経験から収集したデータの規則性や相違性などに気づくようになることもあります.この様にしてデータに対する観察力が養われてくると,データの性質を分かりやすく表現したいと考えるようになります.とくに現代社会では,自然科学や社会科学などの分野を問わず,統計的な思考が要求される時代です.IT情報化社会では,なおさら統計的な思考と統計的な数字によって,私達の意識決定がなされています.
1.1. 統計的データとは.
統計的データとはどのようなものでしようか?
例えば,次のようなデーターがあったとします.
118,148,128,141,139,120,125,123,134,144
これだけでは,たんに10個のデータを並べたに過ぎません.しかし,このデータが血圧値を示す数値であるなら,1つの情報を観察したことになります.また,このデータを男性・女性・健康者・疾患者などで観察すれば,より多くの特性ごとの情報を得ることができます.
このように,私達の知識をもとにデータを観察し,指標としての特性をデータに与え,全体的なデータの性質を考えるとき,これを統計的データ(以下,データと云う)と云います.そして,男性・女性・健康者・疾患者などの特性値を変量または変数と云います.
注釈表示
また,データを観察したとき,その特性には血圧値のように定量的なものと,定性的(質的)なものとがあります.
例えば,
「大きい」,「小さい」,「良い」,「悪い」,「好き」,「嫌い」
など,官能検査や嗜好検査などの多くは定性的データです.この様な定性的データも数量化されて統計的方法の対象となります. 注釈表示
また,データはその特性によって,連続量と離散量に分けられます.例えば,日本人男性の大多数の血圧は110~180mmHgの範囲で,どのような値でもとるところから,血圧値は連続量と云えます.
この血圧値を図1のように,ある範囲の間隔で区切って,その割合を数えたら,その度数は離散量と見なされます.
同様に,血圧値を図2のように分類し脳卒中発生の頻度を求めると,血圧値を質的な特性によって分類したことになり、分類変量と呼ばれます.
| 変量(血圧値) | 度数(人数) |
| 90-109 mmHg | 5 |
| 110-129 | 30 |
| 130-149 | 35 |
| 150-169 | 7 |
| 170-189 | 5 |
| 血圧を一定間隔で設定したとき | 整数値でトビトビの度数を離散量と言う |
| 変量(病名 | 度数(人数) |
|---|---|
| 拡張期血圧 | 28 |
| 収縮期血圧 | 17 |
| 境界域血圧 | 13 |
| 正常域血圧 | 3 |
| 血圧値を4群に分けた | 整数値でトビトビの度数を分類量と言う |
これらをまとめると図3のようになります.
図3 データの分類 注釈表示
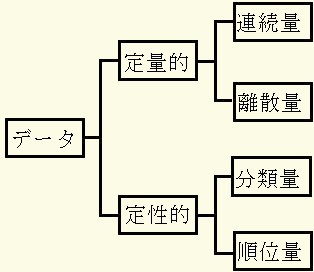
連続量:間隔尺度であり、身長・血圧・コレステロール値などの計測値を指す.
離散量:間隔尺度であり、年齢や身長や体重ごとの計測値(肺活量など)を指す.
分類量:名義尺度であり、内科・外科・耳鼻科の患者数などを指す.
順位量:アンケートなどの「少ない・普通・多い」などの回答を指す.
また,データの変量の数によって1変量,2変量,多変量のデータ,あるいは標本(データを群としてみたとき)と云うこともあります.以上のように,統計的手法の対象となるデータは,特性を付与されているもの,あるいは特性によって分類されているものと云えます.
1.2. 標本と母集団について.
データに特性をあたえ,それを群として観察する時,その群を標本(サンプルまたは試料)と云います.標本は,ある全体集団から無作意にとられたもので,統計的には全体集団の一部を観察しているにすぎません.統計をとる目的は,標本のとられた全体集団を統計的方法によって,観察することであり,この全体集団を母集団と云います.もう少し母集団について説明しましょう.
例えば,先に示した血圧のデータは,僅か10人のデータに過ぎず,その平均値(X-)をもって,日本人の血圧の平均値(μ)とするには,誰しも疑問に思うにちがいありません.しかし,対象人員を100人,1000人,10000人,・・と性別・年齢・地域などに偏りのないように増やして行けば,その平均値(X-)を日本人の平均値(μ)と見なせるようになります. 注釈表示
標本と母集団の関係は図4のように示すことができます.すなわち,その関係は次のように要約することができます.
① 標本は実際に獲られたデータの一群である.
② 標本はある母集団から,無作意にとられたデータある.
③ 標本での分布は,母集団の分布に近似すると考えられる.
④ 母集団は標本からとられた仮設的な集団である.
⑤ 標本からの統計量をもとに,母集団での統計的推察を行う.
図4での標本(1),標本(2)は日本全国から性別や年齢あるいは地域に偏らず,万遍なくとられたデータと仮定すれば,母集団はこの様な標本がいくつも集まったものと考えれば良いのです.もし,国勢調査のように全国民を対象に血圧を測ったとすれば,その血圧値は真に母集団を代表する統計量(記述統計学)に違いありません.
図4 標本と母集団
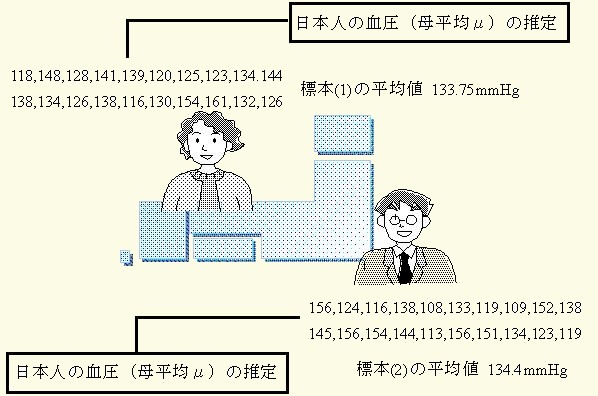
しかし,その様な大量のデータを苦労して集めなくとも,私達は標本から日本人の血圧値を推定(推測統計学)するすべを知っています.
要するに見本(標本)から全体(母集団)を観察することが統計をとる目的の1つなのです.ここで注意すべきことは,標本が母集団の見本である限り,標本は母集団の性質を反映しなければなりません.例えば,ある薬品を購入するときは,その試供品を見て購入薬品の効果を判定するように,標本の分布が正規型であれば,母集団での分布も正規型と判断されます.
しかし,先の血圧の例のように,僅か10人のデータから母集団(日本人の血圧)の分布を仮定することは困難です.ただし,経験的に血圧の分布が正規型あるいはそれに近いことを知っていれば,正規型の仮定は成立します.なお,正規型とは左右対象の釣鐘状に分布しているものを云います.
そこで,対象人員を増やして血圧を測定して行くと,ある範囲で一様に散らばっていた血圧の値が,次第に特定の値(平均値)の周りに集中する,中心化の傾向を示すようになります.
図5はその様子を表しています.
注釈表示
ここでは,主として連続量を例に説明しましたが,離散量のときでも同じことが云えます. 注釈表示
図5 血圧値の分布にみられる中心化の傾向

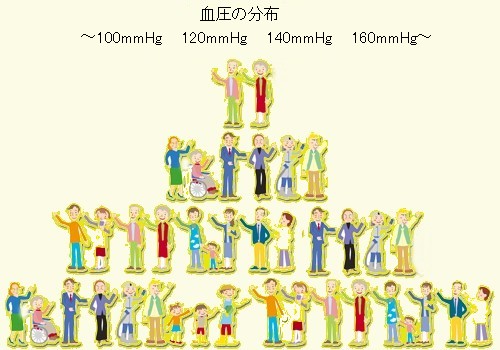
離散量分布に代表される2項分布やポアソン分布の母集団からとられた標本も,やはり母集団の分布に近似します. 注釈表示
しかし,データの数を多くしてゆくと離散量分布も次第に正規分布に近づくのです.このようにに正規分布は正規分布の仮定ももとで行われる統計的方法にとって,非常に大切な分布と云えます.
- 標本での平均値(X-)と母集団での平均値(μ)は区別して用いる.
- 通常,医学での母集団は平均値を(X-)とする1つの実験を繰り返し無数に行ったときに得られる各平均値Xi-(i=1,2,--,∞)の分布と考えれば良い.
- 血圧の分布は年齢・性別・地域・環境・人種・季節・時代・食習慣など多くの要因によって異なっており,1回限りの血圧測定で,その分布を正規型と結論することは出来ない.ここでは,私達の日常生活において血圧の測定がごく身近なものであることを考え例題としている.したがって,血圧の分布を正規型と結論づけている訳ではないので誤解なきよう留意されたい.
- 2項分布とは,ある期間,一定の時間内に病院外来を訪れた患者の性別を調査したとき,男性の割合の度数は2項分布する.そして,その分布は実際に調査した外来患者のうちで男性の占める割合によって決まる.
- ポアソン分布とは,ある期間一定の時間内に病院外来を訪れる患者数を調査したとき,単位時間当りの外来患者数の度数はポアソン分布する.
1.3. 基本的な整理の仕方.
収集したデータは統計をとる目的に応じて,自由に分類しても良いのですが,通常は統計的特性によって分類します.定量的データであれば最初に度数分布を作ってみると良いでしょう.そして,データの分布を確認することが大切です.
1.3.1. 度数分布の作り方.
データは度数分布に整理し,その分布をヒストグラムなどを用い視覚的に確認します.これがデータ整理の第一歩です.「例題」を参考に学習して下さい.
| 級番号 | 級 間 | 中央値 | 度 数 | 累積度数 | 相対度数 |
|---|---|---|---|---|---|
| 1 | A0<=X<A1 | A1 | F1 | F1 | F1/N |
| 2 | A1<=X<A2 | A2 | F2 | F1+F2 | (F1+F2)/N |
| . | . | . | . | . | . |
| K | Ak-1<=X<Ak | Ak | Fk | F1+F2+..+Fk | Fk/N |
| データの個数 | 30~50 | 50~150 | 100~250 | 250~ |
| 級数 | 5~7 | 6~10 | 7~12 | 10~20 |
(Ak-A0)i/K+A0
| 変量 | 度 数 | 累積度数 | 相対度数 |
|---|---|---|---|
| X1 | F1 | F1 | F1/N |
| X2 | F2| F1+F2 | F2/N | |
| . | . | . | . |
| Xk | Fk | F1+F2+..+Fk | Fk/N |
| FACTER(B) | ||||||
|---|---|---|---|---|---|---|
| B1 | B2 | .. | Bm | total | ||
| FACTER(A) | A1 | F11 | F12 | .. | F1m | F1. |
| A2 | F21 | F22 | .. | F2m | F2. | |
| : | .. | .. | .. | .. | .. | |
| An | Fn1 | Fn2 | .. | Fnm | Fn. | |
| total | F.1 | F.2 | .. | F.m | N | |
離散量での「度数分布形式」は全データのうちで,ある特性を持つ個体の割合を示すものです.「分割表形式」は全データを要因によって分類します.また,分割表は要因の特性の数によって,2行×2列分割表,m行×2列分割表,m行×n列分割表などにまとめられます.
[例題1]
連続量データとして,健常成人50人の血糖測定値(g/dl)を表1に示します.このデータをもとに度数分布を作ってみましょう.
表1 健常成人の血糖測定値
108, 94, 87, 88, 91, 81, 86, 87, 87, 87
79, 92, 87, 97, 84, 86, 96, 89, 96, 93
92, 89, 79, 94, 79, 70, 82, 89, 93, 89
88,114, 93,102, 92, 82,109, 98, 93,107
96,120,100,103, 87, 87, 82,107, 74, 85
次に、表計算ソフト「エクセル」による結果を示しましたので参考にして下さい.
●分析ツールによる方法
[例題2]
離散量データとして,同業種企業における1週間以上の病欠者の割合を表2に示します.企業毎に分類されたデータの形式を参考にして下さい.
| 企業 | 対象人員 | 病欠者 | 有病率 |
|---|---|---|---|
| A | 526 | 15 | 2.85% |
| B | 251 | 14 | 5.57% |
| C | 496 | 20 | 4.03% |
| D | 303 | 4 | 1.32% |
| 計 | 1576 | 53 | 3.36% |
[例題3]
離散量データのうち分割表形式として,実薬投与群と偽薬投与群における有効・無効の評価を表3に示します.
| 有効 | 無効 | |
| 実薬群 | 15 | 5 |
| 偽薬群 | 5 | 18 |
実薬と偽薬投与群の有効・無効の割合は,2×2分割表の形式にまとめられています.
1.3.2. ヒストグラムの作り方.
度数分布において,各級に属する個体の度数に比例するように矩形を描きます.離散量であっても,変量自体を級代表と考えヒストグラムとして表現することができます。
ヒストグラムでは、
①データの分布の様子 ②データの散布の様子 ③データの分布の歪み ④デーだの分布の尖りと峰の様子 ⑤異常値の有無などを観察します.
[ヒストグラムの一般形式]
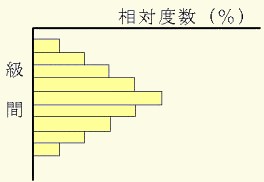
[例題4]
血糖測定値(例題1)を用いて,ヒストグラムを作ってみます.
次に、表計算ソフト「エクセル」による結果を示しましたので参考にして下さい.
● 分析ツールによる方法
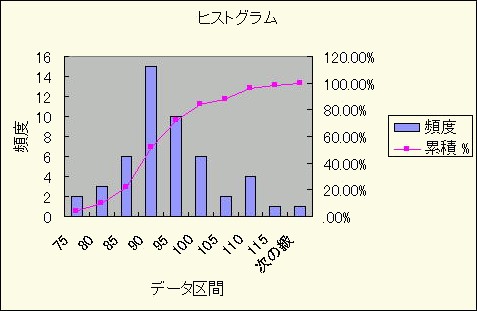
図6は血糖測定値(例題1)の度数分布から求めたヒストグラムです.
級数を10とする血糖値のヒストグラムはやや右に裾を引く尖鋭型を示します.
図6 血糖測定値(例題1)のヒストグラム
1.3.3. 正規確率紙の使い方.
正規確率紙は横軸が等間隔に,縦軸が確率f(x) で目盛られた不等間隔のグラフ用紙です.
注釈表示
このf(x)はf(-∞)=0:f(0)=0.5:f(∞)=1 であり,0≦f(x)≦1の条件からなるf(x)とxとの関係は座標軸上で直線となります.したがって,確率紙上で直線であれば正規分布と見ることができます.
- 正規確率紙は市販品を使用すると便利である.使用方法などは市販説明書を参考にされたい。
- 正規確率紙では縦軸の統計量目盛りと直線になる分布線の交点と一致する横軸目盛規から,平均値(X-)と標準偏差(s)を求めることがきます.
- データ数(n)が小さいときはデータを大きさの順に並べ,それに番号を付けて,その値を横軸上に目盛ります.その値に対する相対累積度数(%)は,100i/(n+1)として縦軸上にプロットします.
- 例えば,次のような大きさの順に並べた9個のデータがあれば,
(1)10,(2)15,(3)20,(4)25,(5)30,(6)35,(7)40,(8)45,(9)50
その相対累積度数は100i/(9+1)=10iから,10%,20%,・・・,90%となります.したがって,縦軸の相対累積度数10%と横軸のデータ10の交点,20%と15の交点,30%と20の交点,・・・,90%と50の交点を結べば良いのです.
1.3.4. データの変換.
度数分布(ヒストグラム・正規確率紙)などで,非正規型の分布を示す連続量のときは,適当なデータ変換によって正規分布に近づける必要があります.データの変換は経験的に行われることが多く,ある程度の試行錯誤が伴います.しかし,一般にはヒストグラムと正規確率紙の分布型の関係から,どの様な変換が適しているか,大体の検討をつけることができます.ただし,必要以上の変換はデータ本来の特性を歪める恐れがあるので注意しなければなりません.
正規確率上の分布において,一般に分布が,
凸のときは、SQRT(x),log(x),log(x-c)
凹のときは、X^2、X^3、10^x
を用いて検討すると良いでしょう. 注釈表示
なお,2項分布やポアソン分布などでの出現率(%)に関するデータ変換については2章(2.2. 正規分布)で説明します.
- データ変換によっても正規分布近似が得られないときは,
(a)データの数が過少でないか? (b)データの収集方法に誤りはないか? (c)統計的にデータの分類が不適当でないか? などを再検討する必要があります. - 統計的に適切なデータであるが,正規分布近似が得られないときは「ノンパラメトリック法」の選択を考えます.
戻る 次へ 目次へ TOPへ