９章（雑記）

戻る　　　　　次へ　　　　　目次へ

9.4.3.　因子分析について。
医学と統計(15)投稿から。

因子分析は多くの変数から共通する因子を求めるもので、変数間の相関関係から導くことになります。
医学では主成分分析の方が扱いやすく適用事例も多いようですが、心理学の分野では因子分析が多用され、根強い人気のようです。
簡単な事例（表1）をもとに、統計解析環境「R」での方法を以下に示します。

表1　アンケート調査での評価点
（主成分分析の例題に変数を加えた）

表1のデータは少数ですので次により「R」に取り込みます。
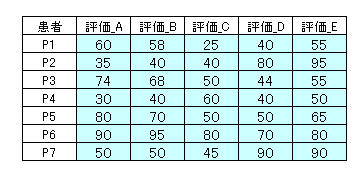
（大標本ではMS-Excelなどを利用して取り込むと良いでしょう）

dat<- matrix(c(
60, 58, 25, 40, 55,
35, 40, 40, 80, 95,
74, 68, 50, 45, 55,
30, 40, 60, 40, 50,
80, 70, 50, 50, 65,
90, 95, 80, 70, 80,
50, 50, 45, 90, 90 ), nrow=7, ncol=3, byrow=TRUE )
colnames(dat)<- c("評価_A", "評価_B", "評価_C", "評価_D", "評価_E")
rownames(dat)<- c("P1", "P2", "P3", "P4", "P5", "P6", "P7")
dat

データを「R」に取り込むことが出来れば次により因子分析を行います。
まずは、
最尤度法による因子分析。

evalu<- factanal( dat, factors = 2, rotation="none", score="regression" )
evalu

rotation は回転方法の指定で、"none"、"varimax"、"promax"　を指定出来ます。
ここでは回転を指定していません。(rotation="none")、
回転には、
直交回転の"varimax"、斜交回転の"promax"があり、どちらを選ぶか迷うなら、
最近、急速にその使用頻度が増加している斜交回転の"promax"をチョイスして見てはどうでしょうか。

出力結果は次の通りです。
*****
> evalu<- factanal( dat, factors = 2, rotaition="none", score="regression" )
> evalu
Call:
factanal(x = dat, factors = 2, scores = "regression", rotaition = "none")

Uniquenesses:

評価_A 評価_B 評価_C 評価_D 評価_E

0.076 0.005 0.658 0.005 0.057

Loadings:

..... Factor1 Factor2

評価_A. 0.955 -0.114

評価_B 0.996 .....

評価_C 0.573 0.114

評価_D 0.997 .....

評価_E 0.971 .....

..... Factor1 Factor2

SS loadings 2.232 1.967

Proportion Var 0.446 0.393

Cumulative Var 0.446 0.840

*****

出力結果から、
"Uniquenesses"は独立因子のことで、因子負荷量（Loadings）で説明できなかった情報の比率です。
この比率を見ると「評価_C」の独立因子が最も大きいことが分かります。
共通因子で負荷量の大きいのは、
”評価_A”、”評価_B”、”評価_D”、”評価_E”であり、第１主成分でこのデータの情報を説明出来ることになります。

最後に、
”SS loadings”（寄与度）、”Proportion Var”（寄与率）、”Cumulative Var”（累積寄与率）が出力されており、
第２因子（Factor2）で全体の情報の84％を説明出来ることを表しています。

因子散布図は次により作成します。
biplot(evalu$scores, evalu$loading)

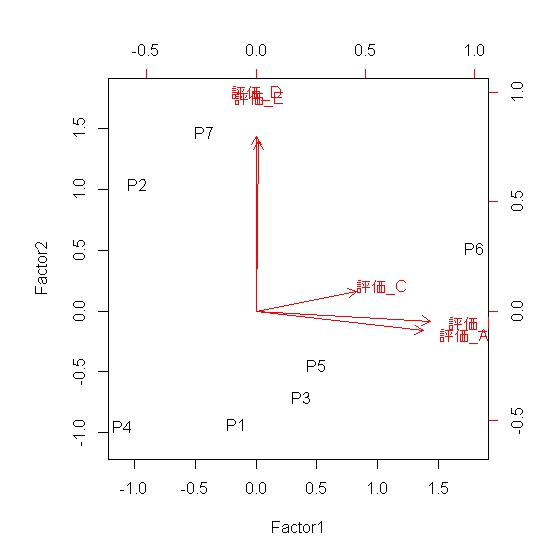
散布図の布置（ポジショニング）から、患者（P)とアンケート評価の関係を読み解くと良いでしょう。

因子分析では、主因子法が定番の様な感があります。例えば、
チョット古い（1995～1999）のですが、心理学研究（教育心理学研究）での各種因子分析法の使用頻度を見ると
次のようになっていました。
　・主因子法　61.5％　・主成分分析　27.7％　・最尤度法　0.8％
　・直交回転（バリマックス法　68.5％、プロクラステス法　3.8％）
　・斜交回転（プロマックス法　18.5％、　オブリミン法　1.5％）

最近では、
「主因子法→プロマックス斜交回転」が急速に増加していますので、以下に主因子法の実行結果を示しておきます。

主因子法（プロマックス回転）の方法
******
library(psych)
evalu1 <- fa(r=dat, nfactors=2 ,rotate="promax", fm="pa", scores=T)
print(evalu1,digits=2,cut=0.1,sort=TRUE)
biplot(evalu1,labels=rownames(dat))

出力結果は次の通りです。
******
Factor Analysis using method = pa
Call: fa(r = dat, nfactors = 2, rotate = "promax", scores = T, fm = "pa")
Standardized loadings (pattern matrix) based upon correlation matrix

..... item PA1 PA2 h2 u2

評価_B 2 1.18 ..... 1.39 -0.39

評価_A 1 0.81 ..... 0.66 0.34

評価_C 3 0.49. 0.12. 0.25 0.75

評価_D 4 ..... 1.06 1.11 -0.11

評価_E 5 ..... 0.92 0.84 0.16

..... PA1 PA2

SS loadings 2.29 1.97

Proportion Var 0.46 0.39

Cumulative Var 0.46 0.85

PA１は第１因子、PA２は第２因子、ｈ２は共通因子、ｕ２は独立因子　です。

因子散布図

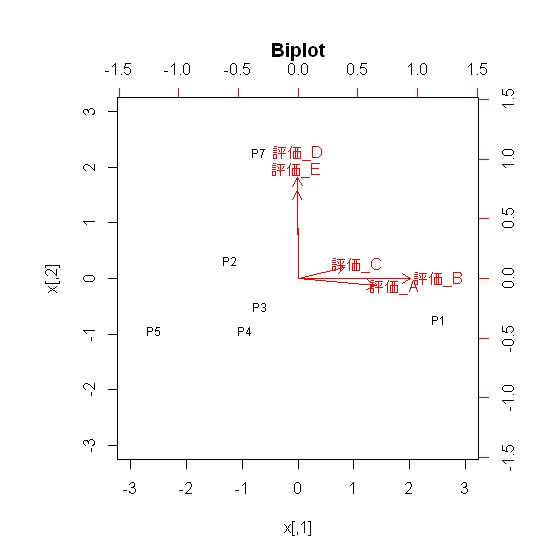
ここでは、単純な少数例題での実行を示したに過ぎません。
大標本になると因子数（nfactors ）をいくらにするか迷うときは、

ns <- fa.parallel(dat)
ns

として、スクリープロットを出力させ決定すれば良いでしょう。

実際の実行に当たっての著者流の手法を示しておきます。

著者流の因子分析（アンケート項目）の手順

　（１）因子分析の前に各項目の平均値と標準偏差を求めておきます。
　（２）「平均値±標準偏差」を求めます。
　（３）「平均値±標準偏差」がとりうる最低値と最高値以上を除きます。
        ５件法（回答が５の場合）では「平均値－標準偏差」≧５、「平均値＋標準偏差」≦1　を除きます。
　（４）第１回目の因子分析は、
   　「主因子法」を選択し、因子数（ nfactors）を適当に定めて因子分析を実行します。
　（５）第２回目は、「SS loadings」≧1.5（見当）、「Cumulative Var」≧50%（見当）で因子数を決め
   　（スクリープロットの変曲点までを採用するなどして）プロマックス回転（promax）を選択して実行します。
　（６）出力結果から、共通性の著しく低い項目をチェックし、各因子の負荷量の著しく小さい項目を除きます。
　（７）除いた項目について、第３回目の因子分析（主因子法、プロマックス回転）を行います。

この様に、
試行錯誤を繰り返し、散布図（biplot）の布置（ポジショニング）から因子の解釈と命名をすれば良いでしょう。

戻る     次へ      目次へ     TOPへ