戻る　　　　　次へ　　　　　目次へ

9.4.2. 主成分回帰分析（回帰主成分分析）の方法について。
医学と統計(55) (56)投稿から。

目的変数(Y)を説明変数(X)で説明しようとするなら重回帰モデルを考えます。しかし、多重共線性など説明変数間の相関が高い （例えば、時系列データ）と重回帰分析をおこなってもほとんど目的を果たせないことがあります。
この様な場合、主成分分析の特性値を説明変数として重回帰分析をおこなった方が良さそうです。
例えば、
表１のデータの様な場合です。

表1：目的変数と従属変数からなるデータ

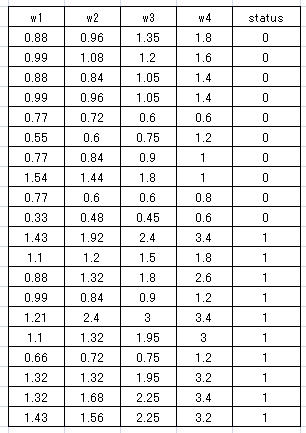
表1 の変数(status)は目的変数であり、ここでは、細胞とか微生物とか何らかの計測値の結果、例えば、 細胞発育状態(good＝０, poor＝１)を、そして、「w1〜w4」は週単位などの時間を表しています。
当然、計測時「w1〜w4」間には高い相関関係があります。このデータについて主成分分析をおこなってみましょう。

主成分分析は統計解析環境「R}では、次の様になります。

dat<- matrix( c(

0.88,	0.96,	1.35,	1.8,	0,
0.99,	1.08,	1.20,	1.6,	0,
0.88,	0.84,	1.05,	1.4,	0,
0.99,	0.96,	1.05,	1.4,	0,
0.77,	0.72,	0.60,	0.6,	0,
0.55,	0.60,	0.75,	1.2,	0,
0.77,	0.84,	0.90,	1.0,	0,
1.54,	1.44,	1.80,	1.0,	0,
0.77,	0.60,	0.60,	0.8,	0,
0.33,	0.48,	0.45,	0.6,	0,
1.43,	1.92,	2.40,	3.4,	1,
1.10,	1.20,	1.50,	1.8,	1,
0.88,	1.32,	1.80,	2.6,	1,
0.99,	0.84,	0.90,	1.2,	1,
1.21,	2.40,	3.00,	3.4,	1,
1.10,	1.32,	1.95,	3.0,	1,
0.66,	0.72,	0.75,	1.2,	1,
1.32,	1.32,	1.95,	3.2,	1,
1.32,	1.68,	2.25,	3.4,	1,
1.43,	1.56,	2.25,	3.2,	1

), ncol=5, nrow=20, byrow=T)
colnames(dat)<- c("w1","w2","w3","w4","status")
dat
dat.pc<- princomp(dat, cor=TRUE)
summary(dat.pc, loadings=TRUE)
round(dat.pc$scores, 2)
biplot(dat.pc)

図1　主成分散布図(biplot)

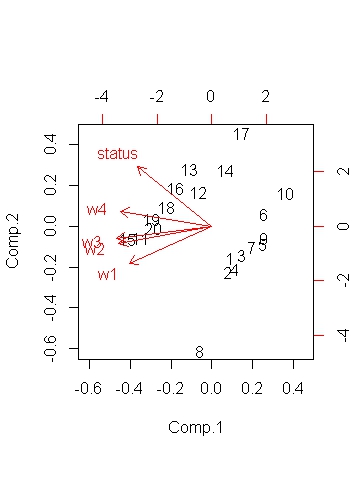
図１では明らかに２つの群に分かれており特徴的な散布図です。
主成分回帰(PCR)は、
ここでの COMP-1 の主成分スコアを説明変数として重回帰型分析を行ったものです。
ここでは、目的変数(status)が「０」と「１」の２値ですので、logistic 回帰分析を適用します。
「R」では次により実行することが出来ます。

dat<- as.data.frame(dat) pcr<- princomp ( dat , cor = TRUE )
summary ( pcr , loading=TRUE )
comp.1<- pcr$scores [ , 1 ]
logit.model<- glm ( status ~ comp.1, binomial , data=dat)
summary ( logit.model )

この実行結果は表2 の様になります。

表2 出力結果

Coefficients:	Estimate	Std. Error	z value	Pr(>|z|)	..
(Intercept)	0.3589	0.7959	0.451	0.6520	..
comp.1	-1.5474	0.6696	-2.311	0.0208	*

---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

目的変数(status)と説明変数(w1〜W4)の関係は第1主成分スコアーを説明変数とした logistic 回帰モデルによって、 細胞発育状態 ( good=0 , poor=1 ) の予測を行うものでした。
ここでは、Logistic 回帰モデルへの当てはめですので、その予測式は、
f(X)=exp ( α＋βX )／(1＋exp(α＋βX ) ) ＝exp ( 0.359＋(−1.5474)* X )／( 1＋exp (0.3589＋(−1.5474)* X ）

（「X」 は comp.1 の score です）

「R」では fitted ( logit.model ) で 予測値（status）を求められます。status の判定は「0.5 以上＝１」とします。

通常、重回帰型分析は予測モデル式を推定するものですが、医学では重回帰型モデルによる未知変数の予測よりも説明変数の 統計学的な有意性を目的に重回帰型分析を行うことが多いようです。
本来は、未知サンプルを回帰式に当てはめたときの予測の良いモデルを求める事にあります。また、多重共線性に問題はないかを 問いましたが、PCR では主成分スコアーを説明変数としており、対応する固有値の高いものを用いておりますので、 多重共線性を気にしなくても良いと言うのが、最近の回帰分析の動向です。しかし、
医学のように統計学的有意変数の select が目的の場合は、多重共線性を無視することは出来ません。この様に、 主成分スコアーなどの factor に基づく回帰分析としては、PCR（Principal Compornent Regression ） や PLS ( Partial Least squares ) があります。
先の PCR では「R」の princomp を用いたプログラムを紹介しましたが、library(pls) では次により分析が出来ます。

library(pls)
summary ( pcr ( status~ ., 3 , data = dat ))
summary ( plsr( status~ ., 3 , data = dat ))
（「R」のバージョンに注意）

係数は次により求める事が出来ます。
「PCR の係数」
p1<- pcr ( status~ ., 3 , data = dat )
round ( p1$coefficients , 3 )

, , 1 comps
....status
w1 0.051
w2 0.095
w3 0.145
w4 0.209

, , 2 comps
....status
w1 -0.093
w2 -0.073
w3 -0.010
w4 0.427

, , 3 comps
....status
w1 0.020
w2 -0.123
w3 -0.039
w4 0.443

「PLS の係数」
p2<- plsr ( status~ ., 3 , data = dat ) round ( p2$coefficients , 3 )

, , 1 comps
....status
w1 0.044
w2 0.086
w3 0.134
w4 0.224

, , 2 comps
....status
w1 -0.060
w2 -0.062
w3 -0.048
w4 0.441

, , 3 comps
....status
w1 0.175
w2 0.084
w3 -0.318
w4 0.505

以上の係数から、第1主成分を用いた重回帰型モデルは、
Y pcr＝0.051W1＋0.095W2＋0.145W3＋0.209W4＋(intercept)
Y pls＝0.044W1＋0.086W2＋0.134W3＋0.224W4＋(intercept)

となり、Y 値が「1」に近いかどうかで当てはめの正誤を判断します。
しかし、「R]では、fitted() 関数で、次により予測値が得られます。

PCR の第1主成分（ 1 comps ）を使用。
p1<- pcr ( status~ ., 1 , data = dat )
b1<- coef(p1, ncomp = 1, intercept = TRUE)
round(b1, 3)
round(p1$fitted, 1)

PLS の第1主成分（ 1 comps ）を使用。
p2<- plsr ( status~ ., 1 , data = dat )
b2<- coef(p2, ncomp = 1, intercept = TRUE)
round(b2, 3)
round(p2$fitted, 1)

戻る     次へ      目次へ     TOPへ